 por Fabio Wanderley » Sex Mar 23, 2012 13:13
por Fabio Wanderley » Sex Mar 23, 2012 13:13
Olá, pessoal. Estou no início do curso de Cálculo I e estudei até Limite Fundamental. Alguém pode me ajudar a resolver esse limite (lembrando que não estudei derivada)?

Tenho outra dúvida também: Posso multiplicar uma indeterminação por zero, resultando em zero? (Isso pq cheguei ao limite de um produto, em que há uma indeterminação sendo multiplicada por sen 0)
Obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Sex Mar 23, 2012 15:16
por MarceloFantini » Sex Mar 23, 2012 15:16
Você já estudou o teorema do confronto?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Sex Mar 23, 2012 17:44
por Fabio Wanderley » Sex Mar 23, 2012 17:44
MarceloFantini escreveu:Você já estudou o teorema do confronto?
Ahhh, vc citou e eu revisei.. acho que entendi mais ou menos agora.. "se x tiver limite 0 em 0 e se sen (1/x) for limitada, então o produto 0 . sen (1/x) terá limite 0 em 0"
É isso o caminho para o exercício né?
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por MarceloFantini » Sex Mar 23, 2012 19:43
por MarceloFantini » Sex Mar 23, 2012 19:43
Mais ou menos. Sabemos que
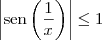
, logo
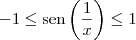
. Daí,
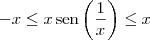
. Vê agora?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Fabio Wanderley » Sex Mar 23, 2012 19:54
por Fabio Wanderley » Sex Mar 23, 2012 19:54
MarceloFantini escreveu:Mais ou menos. Sabemos que
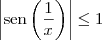
, logo
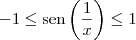
. Daí,
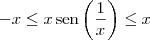
. Vê agora?
Perfeito! Agora enxerguei o teorema do confronto! E caí na real que a função seno é limitada!!
Muito obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
 por LuizAquino » Sáb Mar 24, 2012 02:34
por LuizAquino » Sáb Mar 24, 2012 02:34
Fabio Wanderley escreveu:Perfeito! Agora enxerguei o teorema do confronto! E caí na real que a função seno é limitada!!
Se você desejar ver o Teorema do Confronto aplicado ao cálculo de outro limite trigonométrico, por favor assista a videoaula "07. Cálculo I - Limites Trigonométricos" que está disponível em meu
canal no YouTube.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Wanderley » Sáb Mar 24, 2012 13:01
por Fabio Wanderley » Sáb Mar 24, 2012 13:01
LuizAquino escreveu:Fabio Wanderley escreveu:Perfeito! Agora enxerguei o teorema do confronto! E caí na real que a função seno é limitada!!
Se você desejar ver o Teorema do Confronto aplicado ao cálculo de outro limite trigonométrico, por favor assista a videoaula "07. Cálculo I - Limites Trigonométricos" que está disponível em meu
canal no YouTube.
Assisti ao vídeo. Melhorou ainda mais minha visão sobre o assunto. Recomendo aos colegas do fórum!
Obrigado!
-

Fabio Wanderley
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Sex Mar 23, 2012 12:57
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Estatística
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite fundamental
por matmatco » Qui Set 01, 2011 11:04
- 6 Respostas
- 3465 Exibições
- Última mensagem por matmatco

Qui Set 08, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite fundamental]
por TheKyabu » Qui Out 25, 2012 18:33
- 1 Respostas
- 1722 Exibições
- Última mensagem por TheKyabu

Qui Out 25, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
-
- Limite fundamental
por Julia Maia » Seg Abr 25, 2016 14:17
- 0 Respostas
- 2085 Exibições
- Última mensagem por Julia Maia

Seg Abr 25, 2016 14:17
Cálculo: Limites, Derivadas e Integrais
-
- Limite Fundamental
por Everton Pire Souza » Dom Abr 30, 2017 23:58
- 0 Respostas
- 2963 Exibições
- Última mensagem por Everton Pire Souza

Dom Abr 30, 2017 23:58
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2385 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






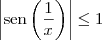 , logo
, logo 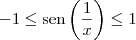 . Daí,
. Daí, 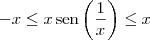 . Vê agora?
. Vê agora?

, logo
. Daí,
. Vê agora?



