 por Gabriel Doria » Sex Mar 23, 2012 00:03
por Gabriel Doria » Sex Mar 23, 2012 00:03
Derive a seguinte equação implícita:
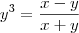
Minha solução:
![y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy} y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy}](/latexrender/pictures/ce9441e8bd4367ee548b23755959301b.png)
Onde foi que eu errei?
-
Gabriel Doria
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Dez 11, 2011 00:42
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nietzsche » Sex Mar 23, 2012 02:14
por nietzsche » Sex Mar 23, 2012 02:14
Na quinta linha quando você distribui o produto era pra ser positivo:
![y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ ->\frac{3y'}{y}=\frac{x+y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ ->\frac{3y'}{y}=\frac{x+y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\](/latexrender/pictures/6763692ec6d00a2b9b447af4ad6fa652.png)
-
nietzsche
- Usuário Parceiro

-
- Mensagens: 99
- Registrado em: Qua Jan 12, 2011 14:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- FATORIAL (ONDE EU ERREI?)
por natanskt » Qui Dez 02, 2010 17:33
- 3 Respostas
- 1942 Exibições
- Última mensagem por alexandre32100

Sex Dez 03, 2010 14:24
Binômio de Newton
-
- Integral - onde errei?
por dina ribeiro » Sex Mar 16, 2012 18:39
- 7 Respostas
- 3304 Exibições
- Última mensagem por dina ribeiro

Dom Mar 18, 2012 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Integral - onde errei?
por dina ribeiro » Sex Mar 23, 2012 21:03
- 1 Respostas
- 1074 Exibições
- Última mensagem por MarceloFantini

Sex Mar 23, 2012 21:10
Cálculo: Limites, Derivadas e Integrais
-
- aonde foi que eu errei ajuda aew!!?(polinomios)
por Fabricio dalla » Sáb Abr 09, 2011 00:38
- 3 Respostas
- 1824 Exibições
- Última mensagem por Fabricio dalla

Sáb Abr 09, 2011 18:07
Polinômios
-
- P.A(Errei todas as resoluçoes desses exercicios de P.A)
por Dalila » Sex Nov 14, 2008 17:33
- 2 Respostas
- 9304 Exibições
- Última mensagem por Cleyson007

Qua Jun 10, 2009 13:06
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
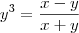
![y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy} y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy}](/latexrender/pictures/ce9441e8bd4367ee548b23755959301b.png)

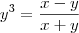
![y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy} y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ \frac{3y'}{y}=\frac{x-y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ \frac{3y'}{y}=\frac{2y-y'(2x)}{x^2-y^2}\\ \frac{3y'}{y}+\frac{y'2x}{x^2-y^2}=\frac{2y}{x^2-y^2}\\ y'(\frac{3}{y}+\frac{2x}{x^2-y^2})=\frac{2y}{x^2-y^2}\\ y'(\frac{3x^2-3y^2+2xy}{y\cdot(x^2-y^2)})=\frac{2y}{x^2-y^2}\\ y'=\frac{2y^2}{3x^2-3y^2+2xy}](/latexrender/pictures/ce9441e8bd4367ee548b23755959301b.png)

![y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ ->\frac{3y'}{y}=\frac{x+y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\ y^3=\frac{x-y}{x+y}\to\ln{y^3}=\ln(\frac{x-y}{x+y})\to\\ \frac{d[\ln y^3]}{dx}=\frac{d[\ln(x-y)]}{dx}-\frac{d[\ln(x+y)]}{dx}\\ \frac{3\cdot y'}{y}=\frac{1-y'}{x-y}-\frac{1+y'}{x+y}\\ \frac{3y'}{y}=\frac{(1-y')(x+y)-(1+y')(x-y)}{x^2-y^2}\\ ->\frac{3y'}{y}=\frac{x+y-y'(x+y)-[x-y+y'(x-y)]}{x^2-y^2}\\](/latexrender/pictures/6763692ec6d00a2b9b447af4ad6fa652.png)

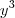 é positivo. Veja os passos do Wolfram:
é positivo. Veja os passos do Wolfram:

