 (relativa ao foguete). Um modelo para a velocidade do foguete a um tempo t é dado pela seguinte equação:
(relativa ao foguete). Um modelo para a velocidade do foguete a um tempo t é dado pela seguinte equação: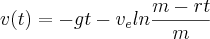
onde g é a aceleração da gravidade, e t não é muito grande. Se g = 9.8 m/s², m = 30000 kg, r = 160 kg/s e
 = 3000 m/s, ache a altitude do foguete 1 minuto após o lançamento.
= 3000 m/s, ache a altitude do foguete 1 minuto após o lançamento.
![= -4.9{t}^{2} + 1500\left[\left(375 - 2t \right)ln\left(\frac{375 - 2t}{375} \right)-\left(375 - 2t \right) \right] + c = -4.9{t}^{2} + 1500\left[\left(375 - 2t \right)ln\left(\frac{375 - 2t}{375} \right)-\left(375 - 2t \right) \right] + c](/latexrender/pictures/d1e31d5888de4c25fbcad3e501533bc7.png)
Resolvendo a integral indefinida cheguei no resultado acima, mas ao aplicar os limites de integração o resultado final dá sempre negativo.


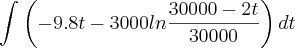

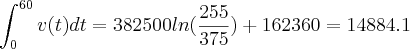

 .
.



