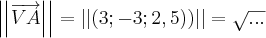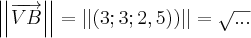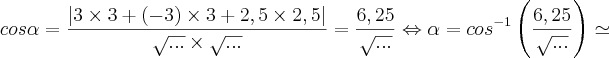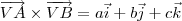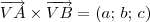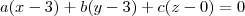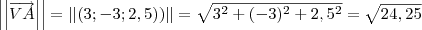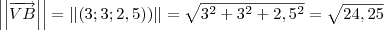por rola09 » Dom Mar 18, 2012 13:40
por rola09 » Dom Mar 18, 2012 13:40
Já tenho algumas respondidas mas deixo aqui o exercício completo para confirmar e pedir ajuda nas restantes.
Num referencial ortonormado está representado uma pirâmide reta, quadrangular regular de vértice V (3,3,0) e base [ABCD].
- A altura da pirâmide é de 2,5 cm
- A base da pirâmide é paralela ao plano XOY
- O vértice D pertence ao eixo OZ
- O vértice A pertence ao plano XOZ
(um pouco mal desenhado mas dá para perceber)
 1 - Identifique as coordenadas dos pontos D, B, C e A.
1 - Identifique as coordenadas dos pontos D, B, C e A.D (0;0;2,5) C (0;6;2,5)
B (6;6;2,5) A (6;0;2,5)
2 - Escreva a equação do plano ABV.Sabendo que a equação do plano é dada por:
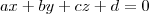
Para determinar a equação temos que descobrir o vetor. É isso certo?
3 - Calcule A 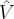 B (em graus e minutos).
B (em graus e minutos).Aqui a única coisa que sei é AB=6 certo?
Tenho algumas dúvidas aqui.
4 - Determine o volume da pirâmide.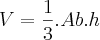

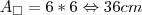
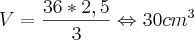
Editado pela última vez por
rola09 em Dom Mar 18, 2012 15:53, em um total de 5 vezes.
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 20:22
por LuizAquino » Dom Mar 18, 2012 20:22
rola09 escreveu:Já tenho algumas respondidas mas deixo aqui o exercício completo para confirmar e pedir ajuda nas restantes.
Num referencial ortonormado está representado uma pirâmide reta, quadrangular regular de vértice V (3,3,0) e base [ABCD].
- A altura da pirâmide é de 2,5 cm
- A base da pirâmide é paralela ao plano XOY
- O vértice D pertence ao eixo OZ
- O vértice A pertence ao plano XOZ
(um pouco mal desenhado mas dá para perceber)
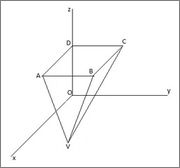
- Tri_ngulo.jpg (3.41 KiB) Exibido 2948 vezes
Na sua figura está faltando apenas o segmento DV.
rola09 escreveu:1 - Identifique as coordenadas dos pontos D, B, C e A.
D (0;0;2,5) C (0;6;2,5)
B (6;6;2,5) A (6;0;2,5)
Ok.
rola09 escreveu:2 - Escreva a equação do plano ABV.Sabendo que a equação do plano é dada por:
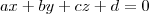
Para determinar a equação temos que descobrir o vetor. É isso certo?
Esse é um caminho: descobrir o vetor normal ao plano.
Para descobrir o vetor normal ao plano, você pode calcular o produto vetorial:
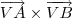
Lembre-se que:
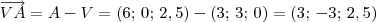
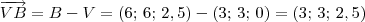
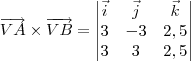
Agora termine a partir daí.
rola09 escreveu:3 - Calcule A 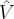 B (em graus e minutos).
B (em graus e minutos).Aqui a única coisa que sei é AB=6 certo?
Tenho algumas dúvidas aqui.
Para calcular o ângulo
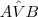
, use a relação abaixo:
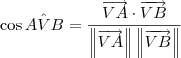
Lembrando que
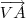
e
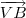
você já calculou no quesito anterior.
Agora termine a partir daí.
rola09 escreveu:4 - Determine o volume da pirâmide.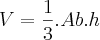

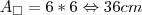
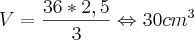
Ok.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rola09 » Dom Mar 18, 2012 21:34
por rola09 » Dom Mar 18, 2012 21:34
LuizAquino escreveu:rola09 escreveu:3 - Calcule A 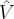 B (em graus e minutos).
B (em graus e minutos).Aqui a única coisa que sei é AB=6 certo?
Tenho algumas dúvidas aqui.
Para calcular o ângulo
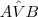
, use a relação abaixo:
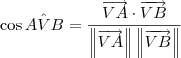
Lembrando que
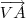
e
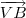
você já calculou no quesito anterior.
Agora termine a partir daí.
Será isto:
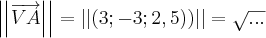
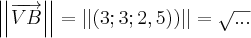
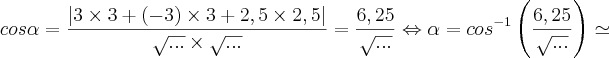
LuizAquino escreveu:rola09 escreveu:2 - Escreva a equação do plano ABV.Sabendo que a equação do plano é dada por:
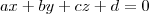
Para determinar a equação temos que descobrir o vetor. É isso certo?
Esse é um caminho: descobrir o vetor normal ao plano.
Para descobrir o vetor normal ao plano, você pode calcular o produto vetorial:
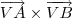
Lembre-se que:
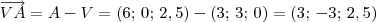
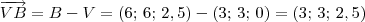
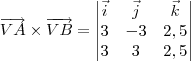
Agora termine a partir daí.
Em relação a este, não estou a perceber como fazer, mas penso que já deva estar saturado com tanta pergunta.
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Dom Mar 18, 2012 21:53
por LuizAquino » Dom Mar 18, 2012 21:53
rola09 escreveu:LuizAquino escreveu:Para calcular o ângulo
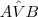
, use a relação abaixo:
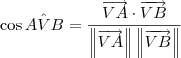
Lembrando que
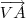
e
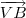
você já calculou no quesito anterior.
Agora termine a partir daí.
Será isto:
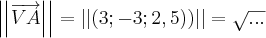
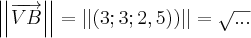
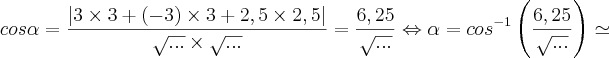
É por aí. Lembrando que as reticências (isto é, "...") serão substituídas pelos cálculos adequados.
rola09 escreveu:LuizAquino escreveu:Esse é um caminho: descobrir o vetor normal ao plano.
Para descobrir o vetor normal ao plano, você pode calcular o produto vetorial:
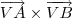
Lembre-se que:
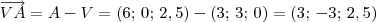
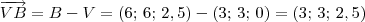
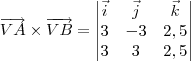
Agora termine a partir daí.
Em relação a este, não estou a perceber como fazer, mas penso que já deva estar saturado com tanta pergunta.
Você sabe calcular o determinante de uma matriz?
Após calcular o determinante da matriz acima, você irá encontrar uma resposta do tipo:
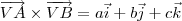
Ou seja, você terá que o vetor normal ao plano será:
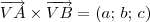
A partir disso, escolhendo um ponto pelo qual o plano irá passar (por exemplo, V = (3; 3; 0)), você pode montar a equação do plano através de:
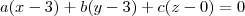
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por rola09 » Dom Mar 18, 2012 22:51
por rola09 » Dom Mar 18, 2012 22:51
Eu não estudo matemática à uns anos e estou a agora a tentar estudar para fazer um exame para terminar a minha escolaridade.
Não me lembro de muita coisa e devido à minha profissão tenho que me sujeitar a estudar sozinho.
Coloquei as reticências porque ainda não consegui chegar aos cálculos corretos dessas raizes.
Mais uma vez quero agradecer a atenção que tem tido e pedir desculpa por qualquer inconveniente
-
rola09
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Mar 12, 2012 15:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cientifico-Natural
- Andamento: cursando
 por LuizAquino » Seg Mar 19, 2012 00:18
por LuizAquino » Seg Mar 19, 2012 00:18
rola09 escreveu:Eu não estudo matemática à uns anos e estou a agora a tentar estudar para fazer um exame para terminar a minha escolaridade.
Não me lembro de muita coisa e devido à minha profissão tenho que me sujeitar a estudar sozinho.
Coloquei as reticências porque ainda não consegui chegar aos cálculos corretos dessas raizes.
Mais uma vez quero agradecer a atenção que tem tido e pedir desculpa por qualquer inconveniente
Você não tem que pedir desculpa. Não há inconveniente algum.
Quanto as raízes, o correto é:
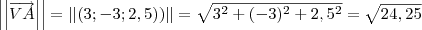
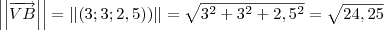
Quanto ao determinante da matriz, eu recomendo que você assista a seguinte videoaula do Nerckie: "Matemática - Aula 20 - Determinantes". Essa videoaula está disponível no canal dele no YouTube:
http://www.youtube.com/nerckieApós assistir a videoaula, tente calcular o determinante. Se tiver alguma dúvida, volte a postar aqui.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Espacial - Pirâmide] Pirâmide de Cartolina
por raimundoocjr » Qui Ago 02, 2012 22:13
- 1 Respostas
- 2701 Exibições
- Última mensagem por MarceloFantini

Qui Ago 02, 2012 23:04
Geometria Espacial
-
- Geometria Analitica Volume da piramide
por Diego Silva » Sex Ago 02, 2013 23:39
- 1 Respostas
- 4173 Exibições
- Última mensagem por mecfael

Dom Ago 18, 2013 22:58
Geometria Analítica
-
- piramide
 por Gir » Ter Set 22, 2009 12:01
por Gir » Ter Set 22, 2009 12:01
- 2 Respostas
- 2850 Exibições
- Última mensagem por Gir

Qua Set 23, 2009 11:02
Geometria Espacial
-
- Pirâmide
 por renataf » Seg Nov 29, 2010 10:06
por renataf » Seg Nov 29, 2010 10:06
- 3 Respostas
- 4567 Exibições
- Última mensagem por fttofolo

Seg Nov 29, 2010 11:09
Geometria Espacial
-
- Pirâmide
por Ani » Dom Dez 05, 2010 15:12
- 4 Respostas
- 3546 Exibições
- Última mensagem por Elcioschin

Sex Dez 10, 2010 21:42
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

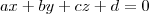
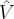 B (em graus e minutos).
B (em graus e minutos).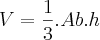

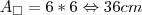
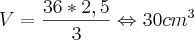


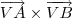
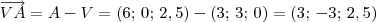
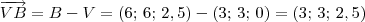
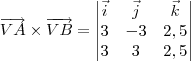
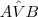 , use a relação abaixo:
, use a relação abaixo: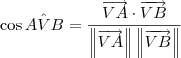
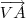 e
e 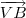 você já calculou no quesito anterior.
você já calculou no quesito anterior.