Quero aproveitar o tópico para colocar mais umas questões de escolha múltipla. Em que a minha resposta se encontra a
BOLT1 - Os planos
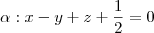
e
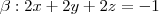
são:
(A) coicidentes
(B) perpendiculares
(c) secantes não perpendiculares(d) estritamente paralelos
2 - Uma equação vetorial da reta que passa em P (-1,2,3) e é perpendicular ao plano
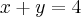
é:
(A)

(B)
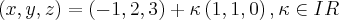 (C)
(C) 
(D)

3 - Considere, em

, a equação trignométrica
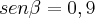
. Em qual destes intervalos esta equação tem uma única solução.
(A)
![\left[-\frac{\pi}{2};\frac{\pi}{2} \right] \left[-\frac{\pi}{2};\frac{\pi}{2} \right]](/latexrender/pictures/d46495c56430eb9a9254c21aa0d02ff2.png) (B)
(B) ![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png)
(C)
![\left[\frac{\pi}{4};\frac{3\pi}{4} \right] \left[\frac{\pi}{4};\frac{3\pi}{4} \right]](/latexrender/pictures/6ed8d7cd7cd9a9d3bdfd5da6df309613.png)
(D)
![\left[-\frac{\pi}{4},\frac{\pi}{4} \right] \left[-\frac{\pi}{4},\frac{\pi}{4} \right]](/latexrender/pictures/d436e25f7064adbcb704f51a48c401b4.png)
4 - Dadas as proposições:
I. Existe um ângulo no IV quadrante cujo co-seno é 2.
II. Sendo

e

dois ângulos do III quadrante tem-se que:
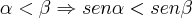
(A) I é verdadeira e II é falsa
(B) São ambas verdadeiras(C) São ambas falsas
(D) II é verdadeira e a I é falsa
5 - Na Figura, está representado o círculo trigonométrico.
Sabe-se que:
•? a recta r é tangente à circunferência no ponto A(1,0)
•? a recta s passa na origem do referencial e intersecta a recta r no ponto P, cuja ordenada é -2
•? o ponto Q, situado no segundo quadrante, pertence à recta s
Seja

a amplitude, em radianos, do ângulo orientado, assinalado na figura, que tem por lado origem o semieixo positivo Ox e por lado
extremidade a semi-recta OP.
Qual é o valor de

, arredondado às centésimas?

(A) -1.10
(B) -1.11(C) 1.10
(D) -2



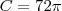
 , temos que:
, temos que: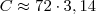
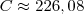
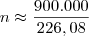
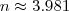

 , então o resultado será diferente.
, então o resultado será diferente.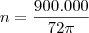
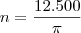
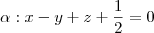 e
e 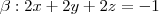 são:
são: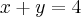 é:
é:
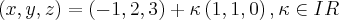


 , a equação trignométrica
, a equação trignométrica 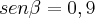 . Em qual destes intervalos esta equação tem uma única solução.
. Em qual destes intervalos esta equação tem uma única solução.![\left[-\frac{\pi}{2};\frac{\pi}{2} \right] \left[-\frac{\pi}{2};\frac{\pi}{2} \right]](/latexrender/pictures/d46495c56430eb9a9254c21aa0d02ff2.png)
![\left[0,\pi \right] \left[0,\pi \right]](/latexrender/pictures/401598234817b1f8eabc57f81da171d0.png)
![\left[\frac{\pi}{4};\frac{3\pi}{4} \right] \left[\frac{\pi}{4};\frac{3\pi}{4} \right]](/latexrender/pictures/6ed8d7cd7cd9a9d3bdfd5da6df309613.png)
![\left[-\frac{\pi}{4},\frac{\pi}{4} \right] \left[-\frac{\pi}{4},\frac{\pi}{4} \right]](/latexrender/pictures/d436e25f7064adbcb704f51a48c401b4.png)
 e
e  dois ângulos do III quadrante tem-se que:
dois ângulos do III quadrante tem-se que: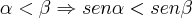

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.