por Adilson » Sáb Jun 13, 2009 00:44
por Adilson » Sáb Jun 13, 2009 00:44
-
Adilson
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 06, 2009 00:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Sáb Jun 13, 2009 21:55
por Molina » Sáb Jun 13, 2009 21:55
Adilson escreveu: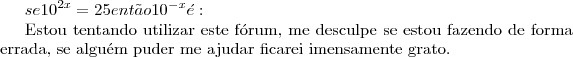
Bem vindo ao forum, Adilson!
Você nao precisa na frase toda usar o Editor de Fórmular, basta usar nas expressões matemáticas, ok?
Sobre sua dúvida acho que o modo mais fácil é usando logaritmo.
Aplicando log em ambos os lados de
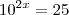
ficamos com:
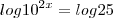
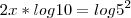
(propriedade do expoente de log/fatoração de 25)
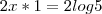
(propriedade de logaritmando e base iguais)
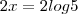
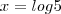
Descobrimos o valor de x, agora substituimos em
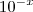
:
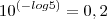
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adilson » Dom Jun 14, 2009 10:54
por Adilson » Dom Jun 14, 2009 10:54
Puxa...Valeu pela ajuda, eu não sabia por onde começar..
E me desculpe, ainda estou aprendendo a utilizar o editor
Brigadão
-
Adilson
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 06, 2009 00:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
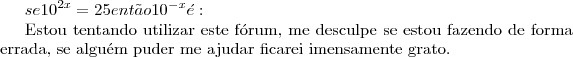



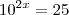 ficamos com:
ficamos com: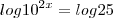
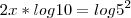 (propriedade do expoente de log/fatoração de 25)
(propriedade do expoente de log/fatoração de 25)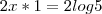 (propriedade de logaritmando e base iguais)
(propriedade de logaritmando e base iguais)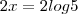
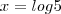
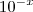 :
: