 por ginrj » Qui Jun 11, 2009 15:52
por ginrj » Qui Jun 11, 2009 15:52
opa, estava fazendo uns exercicios e me deparei com uma questao que me gerou grande duvida.
é do COlegio Naval de 1997
O aluno Mauro, da 8° série de um certo colégio, para resolver a equação:

, no conjunto dos números reais, observou que

e que o segundo membro da equação é um produto notável. Desse modo, concluiu que

é igual a:
(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
ja identifiquei o produto notavel, ja refiz a equação inumeras vezes e nao cheguei a nenhum resultado listado acima, tambem nao entendi a parte final do problema ^^, 2x+1^2 , gostaria de uma ajudinha =D, para eu conseguir resolver o problema, vlww grande abraço
Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
 por Cleyson007 » Qui Jun 11, 2009 16:29
por Cleyson007 » Qui Jun 11, 2009 16:29
Boa tarde Ginrj!
Estou resolvendo e encontrando a alternativa
b como resposta.

Só que estou calculando
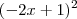
. Confira se a questão foi digitada corretamente.

Você tem o gabarito da questão?
Se tiver o gabarito, coloque a alternativa correta no fórum, a fim de facilitar a vida de quem se dispõe a ajudá-lo.
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por ginrj » Qui Jun 11, 2009 17:24
por ginrj » Qui Jun 11, 2009 17:24
no gabarito diz letra C, numero 5, eu calculei com o sinal oposto tbm, nenhum da 5 , Vlww abç
Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
 por Molina » Qui Jun 11, 2009 19:38
por Molina » Qui Jun 11, 2009 19:38
Deixa eu ver se entendi.
Ele disse que
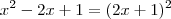
Se for isso acho que está errado, pois na verdade

E agora, qual o próximo passo?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Jun 11, 2009 22:37
por Cleyson007 » Qui Jun 11, 2009 22:37
Boa noite!
Agora entendi o problema. Vejamos:
O polinômio é o seguinte:
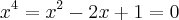
. Desenvolvendo fica assim:
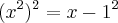
-->
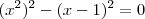
. Por diferença de dois quadrados temos:
![[{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0 [{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0](/latexrender/pictures/b8caa6ea20a85f3fc86728eb3e451f22.png)
-->
![[{x}^{2}-x+1][{x}^{2}+x-1 [{x}^{2}-x+1][{x}^{2}+x-1](/latexrender/pictures/6eb39c1a728c45c36a953efd093a0203.png)
![]=0 ]=0](/latexrender/pictures/bc67c8cd970921adaff9f37f636aae34.png)
Note que somente o lado direito da igualdade atende as condições do problema (números reais).

-->
![x=\frac{-1+\sqrt[2]{5}}{2} x=\frac{-1+\sqrt[2]{5}}{2}](/latexrender/pictures/65cc12fac07d3076cb9d26af6a346433.png)
![2x=-1+\sqrt[2]{5} 2x=-1+\sqrt[2]{5}](/latexrender/pictures/b1dfcb5e7b8bc6a5b3f346975fadca02.png) Elvevando ambos os lados ao quadrado, obtemos:
Elvevando ambos os lados ao quadrado, obtemos: 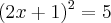
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por ginrj » Sáb Jun 13, 2009 18:34
por ginrj » Sáb Jun 13, 2009 18:34
cleyson e molina, quando chegar em casa vou tentar resolver, ^^ cheguei na parte do -1+raiz de 5 sobre 2 mais nao pensei em elevar os dois termos ao quadrado =p, vlwww aii pessoall

Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - como montar a equação desse problema?
por _Manu » Qua Jul 04, 2012 03:37
- 7 Respostas
- 13216 Exibições
- Última mensagem por _Manu

Qui Jul 05, 2012 01:49
Sistemas de Equações
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8706 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
-
- [ PROBLEMA ] Equação
por gabrielMAT » Qua Out 19, 2011 16:45
- 2 Respostas
- 1844 Exibições
- Última mensagem por gabrielMAT

Qua Out 19, 2011 19:58
Sistemas de Equações
-
- Problema de equação
por TiagoFERD » Sáb Mar 10, 2012 09:59
- 2 Respostas
- 1438 Exibições
- Última mensagem por TiagoFERD

Sáb Mar 10, 2012 10:48
Sistemas de Equações
-
- Problema! equação.
por LuizCarlos » Ter Abr 03, 2012 10:59
- 5 Respostas
- 2815 Exibições
- Última mensagem por ednaldo1982

Qua Abr 04, 2012 00:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , no conjunto dos números reais, observou que
, no conjunto dos números reais, observou que  e que o segundo membro da equação é um produto notável. Desse modo, concluiu que
e que o segundo membro da equação é um produto notável. Desse modo, concluiu que  é igual a:
é igual a:


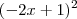 . Confira se a questão foi digitada corretamente.
. Confira se a questão foi digitada corretamente. Você tem o gabarito da questão?
Você tem o gabarito da questão? 

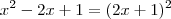



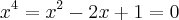 . Desenvolvendo fica assim:
. Desenvolvendo fica assim: 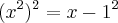 -->
--> 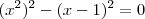 . Por diferença de dois quadrados temos:
. Por diferença de dois quadrados temos: ![[{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0 [{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0](/latexrender/pictures/b8caa6ea20a85f3fc86728eb3e451f22.png) -->
--> ![[{x}^{2}-x+1][{x}^{2}+x-1 [{x}^{2}-x+1][{x}^{2}+x-1](/latexrender/pictures/6eb39c1a728c45c36a953efd093a0203.png)
![]=0 ]=0](/latexrender/pictures/bc67c8cd970921adaff9f37f636aae34.png)
 -->
-->![x=\frac{-1+\sqrt[2]{5}}{2} x=\frac{-1+\sqrt[2]{5}}{2}](/latexrender/pictures/65cc12fac07d3076cb9d26af6a346433.png)
![2x=-1+\sqrt[2]{5} 2x=-1+\sqrt[2]{5}](/latexrender/pictures/b1dfcb5e7b8bc6a5b3f346975fadca02.png)
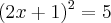

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.