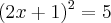é do COlegio Naval de 1997
O aluno Mauro, da 8° série de um certo colégio, para resolver a equação:
 , no conjunto dos números reais, observou que
, no conjunto dos números reais, observou que  e que o segundo membro da equação é um produto notável. Desse modo, concluiu que
e que o segundo membro da equação é um produto notável. Desse modo, concluiu que  é igual a:
é igual a:(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
ja identifiquei o produto notavel, ja refiz a equação inumeras vezes e nao cheguei a nenhum resultado listado acima, tambem nao entendi a parte final do problema ^^, 2x+1^2 , gostaria de uma ajudinha =D, para eu conseguir resolver o problema, vlww grande abraço



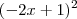 . Confira se a questão foi digitada corretamente.
. Confira se a questão foi digitada corretamente. Você tem o gabarito da questão?
Você tem o gabarito da questão? 

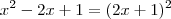



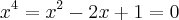 . Desenvolvendo fica assim:
. Desenvolvendo fica assim: 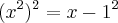 -->
--> 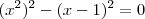 . Por diferença de dois quadrados temos:
. Por diferença de dois quadrados temos: ![[{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0 [{x}^{2}-(x-1)][{x}^{2}+(x-1)]=0](/latexrender/pictures/b8caa6ea20a85f3fc86728eb3e451f22.png) -->
--> ![[{x}^{2}-x+1][{x}^{2}+x-1 [{x}^{2}-x+1][{x}^{2}+x-1](/latexrender/pictures/6eb39c1a728c45c36a953efd093a0203.png)
![]=0 ]=0](/latexrender/pictures/bc67c8cd970921adaff9f37f636aae34.png)
 -->
-->![x=\frac{-1+\sqrt[2]{5}}{2} x=\frac{-1+\sqrt[2]{5}}{2}](/latexrender/pictures/65cc12fac07d3076cb9d26af6a346433.png)
![2x=-1+\sqrt[2]{5} 2x=-1+\sqrt[2]{5}](/latexrender/pictures/b1dfcb5e7b8bc6a5b3f346975fadca02.png)