 Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:Os coeficientes angular e linear da reta 3y-2x=12=0 é?
O triângulo de verticies A(4,3) , B (6,-2) e C (-11,-3) é?Prove.
Obrigado.

 Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
Ola pessoal, não estou conseguido resolver estas continha ,principalmente a do triangulo lá vai elas:
felipeke escreveu:Os coeficientes angular e linear da reta 3y-2x=12=0 é?

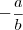 será o angular. Já o coeficiente
será o angular. Já o coeficiente 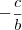 será o linear.
será o linear.felipeke escreveu:O triângulo de verticies A(4,3) , B (6,-2) e C (-11,-3) é? Prove.

Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.