 por Brufofs » Ter Mar 13, 2012 19:37
por Brufofs » Ter Mar 13, 2012 19:37
Dado o triângulo ABC, calcule o perímetro do triângulo ADE,sabendo que CF e BF são bissetrizes dos ângulos C e B respectivamente, AB=11, AC=18 e DE é paralelo a BC:

-
Brufofs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 13, 2012 19:30
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por LuizAquino » Ter Mar 13, 2012 20:15
por LuizAquino » Ter Mar 13, 2012 20:15
Brufofs escreveu:Dado o triângulo ABC, calcule o perímetro do triângulo ADE,sabendo que CF e BF são bissetrizes dos ângulos
C e B respectivamente, AB=11, AC=18 e DE é paralelo a BC:
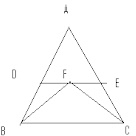
- imagem.jpg (7.7 KiB) Exibido 5100 vezes
Como

e

são bissetrizes, temos que

e

.
Além disso, como

é paralelo a

, temos que

(pois eles são alternos internos) e

(pois eles são alternos internos).
Conclusão: BDF e CEF são isósceles.
Sendo assim, temos que

e

.
Considerando essa informação, tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Brufofs » Ter Mar 13, 2012 21:21
por Brufofs » Ter Mar 13, 2012 21:21
Desculpa, eu acabei fazendo um desenho errado, da uma olhada em como ele realmente é:
Mas o que mais me intriga é que só foram dadas duas informações em números e eu preciso achar o perímetro, como acharia um perímetro com ângulo?
- Anexos
-
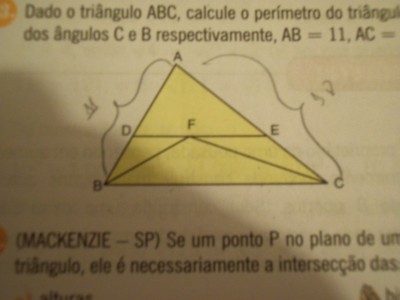
-
Brufofs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 13, 2012 19:30
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por LuizAquino » Qua Mar 14, 2012 14:25
por LuizAquino » Qua Mar 14, 2012 14:25
Brufofs escreveu:Desculpa, eu acabei fazendo um desenho errado, da uma olhada em como ele realmente é:

- figura.JPG (86.68 KiB) Exibido 5088 vezes
O desenho não importa nesse caso. O importante é o texto do exercício.
O texto que você enviou agora está cortado, mas eu presumo que seja o mesmo enviado anteriormente. Desse modo, tudo que disse na mensagem anterior continua válido.
Brufofs escreveu:Mas o que mais me intriga é que só foram dadas duas informações em números e eu preciso achar o perímetro, como acharia um perímetro com ângulo?
Somente com as informações dadas já é possível resolver o exercício.
Considerando tudo que disse na mensagem anterior, podemos criar a seguinte figura.
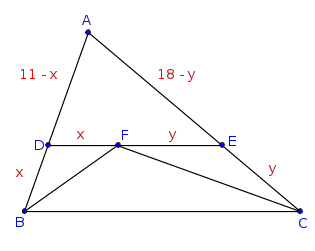
- figura2.png (5.95 KiB) Exibido 5088 vezes
Agora fica fácil determinar o perímetro de ADE.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Brufofs » Qua Mar 14, 2012 14:29
por Brufofs » Qua Mar 14, 2012 14:29
Muito Obrigado
-
Brufofs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 13, 2012 19:30
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Brufofs » Qua Mar 14, 2012 14:46
por Brufofs » Qua Mar 14, 2012 14:46
Daria isso:P=11-X+18-Y+X+Y=
p=29
Porque corta se os x e os y, já que um decada é negativo e o outro positivo.
-
Brufofs
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 13, 2012 19:30
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 17:01
- 8 Respostas
- 6365 Exibições
- Última mensagem por lenda

Qui Jul 19, 2012 15:38
Geometria Plana
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 17:23
- 2 Respostas
- 2071 Exibições
- Última mensagem por lenda

Qua Jul 18, 2012 20:20
Geometria Plana
-
- pontos notáveis do triângulo
por lenda » Qua Jul 18, 2012 20:57
- 2 Respostas
- 1879 Exibições
- Última mensagem por lenda

Qui Jul 19, 2012 14:53
Geometria Plana
-
- Pontos notáveis do triângulo
por Tmartins » Qua Mai 15, 2013 16:01
- 0 Respostas
- 1097 Exibições
- Última mensagem por Tmartins

Qua Mai 15, 2013 16:01
Geometria Plana
-
- Conceitos de pontos notáveis em triângulo
 por alfabeta » Sex Mar 09, 2012 20:53
por alfabeta » Sex Mar 09, 2012 20:53
- 1 Respostas
- 1909 Exibições
- Última mensagem por LuizAquino

Ter Mar 13, 2012 17:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 e
e  são bissetrizes, temos que
são bissetrizes, temos que  e
e  .
. é paralelo a
é paralelo a  , temos que
, temos que  (pois eles são alternos internos) e
(pois eles são alternos internos) e  (pois eles são alternos internos).
(pois eles são alternos internos). e
e  .
.



