 por Flames » Ter Mar 13, 2012 00:10
por Flames » Ter Mar 13, 2012 00:10
Bem pessoal eu tenho aqui uma dúvida que não consigo chegar ao resultado pretendido:

no ponto (2,-3,2)
Eu fiz as derivadas parciais/gradiente algo como

Por fx,fy,fz entende-se a derivada parcial no ponto (2,-3,2)...
O final deveria dar algo como:

E não consegui alcançar tal...
Desculpem algum texto porque latex afffffffffffff
-
Flames
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 12, 2012 23:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Ter Mar 13, 2012 11:47
por LuizAquino » Ter Mar 13, 2012 11:47
Flames escreveu:Bem pessoal eu tenho aqui uma dúvida que não consigo chegar ao resultado pretendido:

no ponto (2,-3,2)
Eu fiz as derivadas parciais/gradiente algo como

Por fx,fy,fz entende-se a derivada parcial no ponto (2,-3,2)...
O final deveria dar algo como:

E não consegui alcançar tal...
Envie a sua resolução para que possamos corrigi-la.
Flames escreveu:Desculpem algum texto porque latex afffffffffffff
O LaTeX é ótimo! Por exemplo, sem o LaTeX, a equação que você escreveu acima seria algo como:
(x^2)/4 + (y^2)/9 + (z^2)/4 = 3
É ruim ler nessa forma de escrita! É muito melhor ler simplesmente:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Flames » Ter Mar 13, 2012 20:46
por Flames » Ter Mar 13, 2012 20:46
O que fiz foi:
achei a derivada parcial em ordem a x
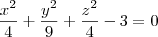
dando a derivada

no ponto (2,-3,2) =

achei a derivada parcial em ordem a y
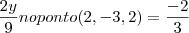
achei a derivada parcial em ordem a z
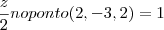
Depois disto fui buscar o ponto (2,-3,2) e substitui em cada derivada parcial juntando no final à formula:

-
Flames
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 12, 2012 23:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Ter Mar 13, 2012 21:07
por LuizAquino » Ter Mar 13, 2012 21:07
Flames escreveu:O que fiz foi:
achei a derivada parcial em ordem a x
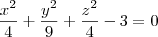
dando a derivada

no ponto (2,-3,2) =

Ok.
Flames escreveu:achei a derivada parcial em ordem a y

no ponto (2,-3,2)
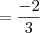
Ok.
Flames escreveu:
no ponto (2,-3,2) = 1
Ok.
Flames escreveu:Depois disto fui buscar o ponto (2,-3,2) e substitui em cada derivada parcial juntando no final à formula:

Ok. Basta continuar a partir daí.
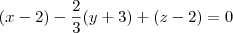


Esta é uma resposta correta. Mas se você quiser obter a resposta apresentada no gabarito, então basta multiplicar ambos os membros da equação por -3.
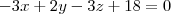
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Flames » Ter Mar 13, 2012 23:15
por Flames » Ter Mar 13, 2012 23:15
LuizAquino escreveu:Flames escreveu:O que fiz foi:
achei a derivada parcial em ordem a x
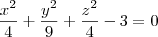
dando a derivada

no ponto (2,-3,2) =

Ok.
Flames escreveu:achei a derivada parcial em ordem a y

no ponto (2,-3,2)
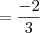
Ok.
Flames escreveu:
no ponto (2,-3,2) = 1
Ok.
Flames escreveu:Depois disto fui buscar o ponto (2,-3,2) e substitui em cada derivada parcial juntando no final à formula:

Ok. Basta continuar a partir daí.
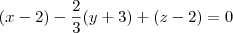


Esta é uma resposta correta. Mas se você quiser obter a resposta apresentada no gabarito, então basta multiplicar ambos os membros da equação por -3.
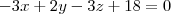
Muito Obrigado algo tão simples eu achei que deveria aparecer directamente na operação... Mais uma vez obrigado pelo seu tempo disponibilizado

-
Flames
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Mar 12, 2012 23:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2943 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- PLANO TANGENTE
por renan_cpime14 » Sáb Out 12, 2013 14:49
- 0 Respostas
- 1227 Exibições
- Última mensagem por renan_cpime14

Sáb Out 12, 2013 14:49
Cálculo: Limites, Derivadas e Integrais
-
- Plano tangente
por carolzinhag3 » Seg Abr 10, 2017 23:11
- 2 Respostas
- 2534 Exibições
- Última mensagem por carolzinhag3

Sex Abr 14, 2017 23:46
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] plano tangente
por Higor Yuri » Seg Jun 18, 2012 12:33
- 1 Respostas
- 3011 Exibições
- Última mensagem por LuizAquino

Ter Jun 19, 2012 11:47
Cálculo: Limites, Derivadas e Integrais
-
- Superfície e Plano Tangente- URGENTE
por leroaquino » Qui Set 17, 2015 19:46
- 2 Respostas
- 2277 Exibições
- Última mensagem por leroaquino

Seg Set 21, 2015 16:10
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 no ponto (2,-3,2)
no ponto (2,-3,2)


 no ponto (2,-3,2)
no ponto (2,-3,2)


no ponto (2,-3,2)


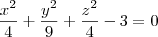
 no ponto (2,-3,2) =
no ponto (2,-3,2) =
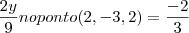
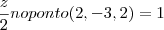


no ponto (2,-3,2) =
no ponto (2,-3,2)
no ponto (2,-3,2) = 1
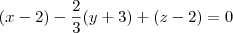


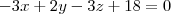

no ponto (2,-3,2) =
no ponto (2,-3,2)
no ponto (2,-3,2) = 1

