 por Wilson de Andrade » Dom Mar 11, 2012 16:08
por Wilson de Andrade » Dom Mar 11, 2012 16:08
Uma curva de deslocamento é formada por duas parábolas f(x) e g(x) com vértices
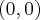
e
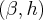
, respectivamente, concordantes no ponto médio
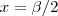
.
Sendo
h o deslocamento máximo em
y e

a posição angular máxima do came no eixo
x (uma volta completa, por exemplo

).
Há duas equações do movimento:
No trecho
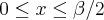
(f(x));
e no trecho
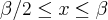
(g(x)).
No trecho
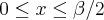

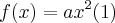
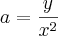
No instante

Portanto:
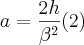
Substituindo (2) em (1):
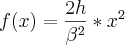
Derivando obtemos a equação da velocidade:

No instante

a velocidade será máxima, portanto:
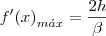
Já no trecho
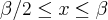

Para a equação da velocidade:

No instante
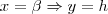
, então:
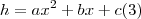
.
Ao mesmo tempo que no instante
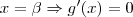
Portanto:

No instante

a velocidade também será máxima, portanto:

Ou seja,

Resolvendo simultaneamente as equações (3), (4) e (5), o autor obtem os seguintes valores para as constantes a, b e c:
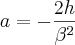


Esta é minha dificuldade, entender como o autor resolveu o sistema para encontrar
a,
b e
c, obtendo as equações definitivas:
![g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right] g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right]](/latexrender/pictures/b1402929247243b4e8aa65ea878eb681.png)
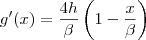
Obrigado.
-
Wilson de Andrade
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 11, 2012 13:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Processos de produção
- Andamento: formado
 por Wilson de Andrade » Seg Mar 12, 2012 00:13
por Wilson de Andrade » Seg Mar 12, 2012 00:13
Enquanto postava esta dúvida fui organizando meu raciocínio, e acho que consegui resolver uma parte:
Igualando a equação (5) a zero,
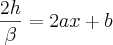
, indicando que

no instante

:
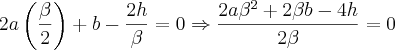
ou
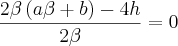

. Isolando b:

.
Substiuindo b na equação (4), que se trata da derivada de g(x) no instante

:


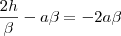
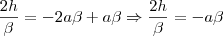
Portanto,
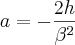
.
Substituindo a no valor de b:


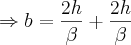
Portanto,

Substituindo a e b na equação (3) para obter c:
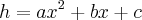
, no instante

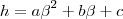
Isolando c:
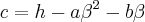


Portanto,

.
Acho que é isso. Agora, fatorar a equação definitiva
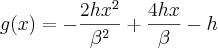
para ela ficar
![g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right] g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right]](/latexrender/pictures/b1402929247243b4e8aa65ea878eb681.png)
eu não sei fazer, sou péssimo em fatoração...
Valeu.
-
Wilson de Andrade
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Mar 11, 2012 13:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia em Processos de produção
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- não sei como chegar na resposta
por Dankaerte » Seg Ago 31, 2009 17:05
- 3 Respostas
- 5785 Exibições
- Última mensagem por Elcioschin

Seg Ago 31, 2009 23:27
Sistemas de Equações
-
- Como chegar na equação
por Rafael16 » Sex Nov 23, 2012 19:12
- 2 Respostas
- 1677 Exibições
- Última mensagem por DanielFerreira

Sex Nov 23, 2012 20:52
Equações
-
- Porcentagem...(como chegar na resposta?)
por Dyego » Sex Mar 26, 2010 13:45
- 1 Respostas
- 4429 Exibições
- Última mensagem por Dan

Sex Mar 26, 2010 16:31
Matemática Financeira
-
- Como chegar a essa função?
por frcol » Sex Jan 30, 2015 14:28
- 1 Respostas
- 1795 Exibições
- Última mensagem por Russman

Dom Fev 01, 2015 14:24
Aritmética
-
- como chegar a formula de tronco de cone
por alinemuller » Ter Mai 11, 2010 17:36
- 0 Respostas
- 1809 Exibições
- Última mensagem por alinemuller

Ter Mai 11, 2010 17:36
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
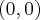 e
e 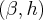 , respectivamente, concordantes no ponto médio
, respectivamente, concordantes no ponto médio 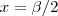 .
. a posição angular máxima do came no eixo x (uma volta completa, por exemplo
a posição angular máxima do came no eixo x (uma volta completa, por exemplo  ).
).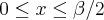 (f(x));
(f(x));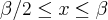 (g(x)).
(g(x)).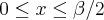

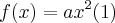
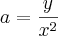

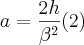
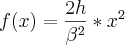

 a velocidade será máxima, portanto:
a velocidade será máxima, portanto: 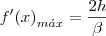
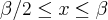


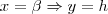 , então:
, então: 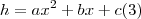 .
.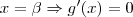

 a velocidade também será máxima, portanto:
a velocidade também será máxima, portanto: 

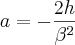


![g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right] g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right]](/latexrender/pictures/b1402929247243b4e8aa65ea878eb681.png)
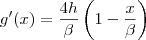


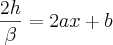 , indicando que
, indicando que 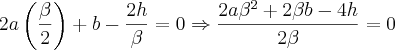
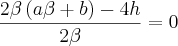
 . Isolando b:
. Isolando b:  .
. :
:

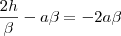
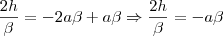

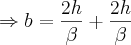
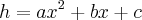 , no instante
, no instante 
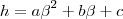
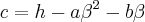


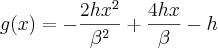
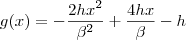
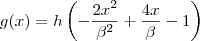
![g(x)=h\left[-2\left(\dfrac{{x}^{2}}{{\beta}^{2}}-\dfrac{2x}{\beta}\right)-1\right] g(x)=h\left[-2\left(\dfrac{{x}^{2}}{{\beta}^{2}}-\dfrac{2x}{\beta}\right)-1\right]](/latexrender/pictures/297dd5cfd334e3453c392b7b0c1cda45.png)
![g(x)=h\left\{-2\left[\left(1 - \dfrac{x}{\beta}\right)^2 - 1\right]-1\right\} g(x)=h\left\{-2\left[\left(1 - \dfrac{x}{\beta}\right)^2 - 1\right]-1\right\}](/latexrender/pictures/26e87d38ffa2beeb53670de871521c44.png)
![g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 2 - 1\right] g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 2 - 1\right]](/latexrender/pictures/672d2fc81e4dfcbdd0a7f1b338d466fa.png)
![g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 1\right] g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 1\right]](/latexrender/pictures/e552f63d6e5a907f38459d5b487ad83d.png)
![g(x)=h\left[1 - 2\left(1 - \dfrac{x}{\beta}\right)^2\right] g(x)=h\left[1 - 2\left(1 - \dfrac{x}{\beta}\right)^2\right]](/latexrender/pictures/46b7e772e62c947be8b9411cc582e929.png)






