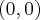 e
e 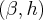 , respectivamente, concordantes no ponto médio
, respectivamente, concordantes no ponto médio 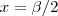 .
.Sendo h o deslocamento máximo em y e
 a posição angular máxima do came no eixo x (uma volta completa, por exemplo
a posição angular máxima do came no eixo x (uma volta completa, por exemplo  ).
).Há duas equações do movimento:
No trecho
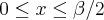 (f(x));
(f(x));e no trecho
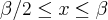 (g(x)).
(g(x)).No trecho
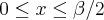

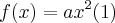
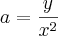
No instante

Portanto:
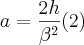
Substituindo (2) em (1):
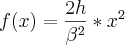
Derivando obtemos a equação da velocidade:

No instante
 a velocidade será máxima, portanto:
a velocidade será máxima, portanto: 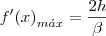
Já no trecho
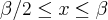

Para a equação da velocidade:

No instante
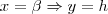 , então:
, então: 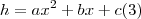 .
.Ao mesmo tempo que no instante
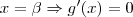
Portanto:

No instante
 a velocidade também será máxima, portanto:
a velocidade também será máxima, portanto: 
Ou seja,

Resolvendo simultaneamente as equações (3), (4) e (5), o autor obtem os seguintes valores para as constantes a, b e c:
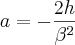


Esta é minha dificuldade, entender como o autor resolveu o sistema para encontrar a,b e c, obtendo as equações definitivas:
![g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right] g(x)=h\left[1-2{\left(1-\frac{x}{\beta} \right)}^{2} \right]](/latexrender/pictures/b1402929247243b4e8aa65ea878eb681.png)
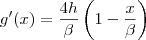
Obrigado.


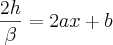 , indicando que
, indicando que 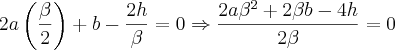
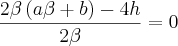
 . Isolando b:
. Isolando b:  .
. :
:

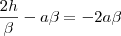
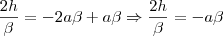

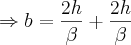
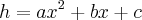 , no instante
, no instante 
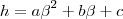
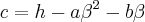


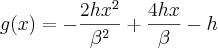
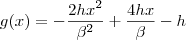
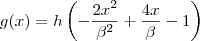
![g(x)=h\left[-2\left(\dfrac{{x}^{2}}{{\beta}^{2}}-\dfrac{2x}{\beta}\right)-1\right] g(x)=h\left[-2\left(\dfrac{{x}^{2}}{{\beta}^{2}}-\dfrac{2x}{\beta}\right)-1\right]](/latexrender/pictures/297dd5cfd334e3453c392b7b0c1cda45.png)
![g(x)=h\left\{-2\left[\left(1 - \dfrac{x}{\beta}\right)^2 - 1\right]-1\right\} g(x)=h\left\{-2\left[\left(1 - \dfrac{x}{\beta}\right)^2 - 1\right]-1\right\}](/latexrender/pictures/26e87d38ffa2beeb53670de871521c44.png)
![g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 2 - 1\right] g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 2 - 1\right]](/latexrender/pictures/672d2fc81e4dfcbdd0a7f1b338d466fa.png)
![g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 1\right] g(x)=h\left[-2\left(1 - \dfrac{x}{\beta}\right)^2 + 1\right]](/latexrender/pictures/e552f63d6e5a907f38459d5b487ad83d.png)
![g(x)=h\left[1 - 2\left(1 - \dfrac{x}{\beta}\right)^2\right] g(x)=h\left[1 - 2\left(1 - \dfrac{x}{\beta}\right)^2\right]](/latexrender/pictures/46b7e772e62c947be8b9411cc582e929.png)
