
Eu fui resolvendo o limite e achei as raízes (x-3).(x +1/2) para o divisor, sendo que na resposta aparece (x-3).(2x +1). Alguém poderia me explicar detalhadamente como isso acontece ?



 , isso significa fazer
, isso significa fazer 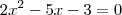 , de onde temos
, de onde temos 
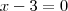 ou
ou 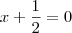 .
.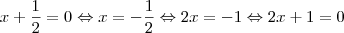
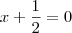 é o mesmo que
é o mesmo que  .
.
Ademir Jose escreveu:
Eu fui resolvendo o limite e achei as raízes (x-3).(x +1/2) para o divisor, sendo que na resposta aparece (x-3).(2x +1).
ant_dii escreveu:Como você disse, você encontrou as raízes de, isso significa fazer 2x^2 - 5x - 3=0, de onde temos
 .
. 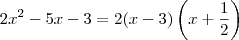
![2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right] 2x^2 - 5x - 3 = (x-3)\left[2\left(x+\dfrac{1}{2}\right)\right]](/latexrender/pictures/5e154778188960f49a64e9b06f2c937c.png)






joaofonseca escreveu:Na pratica é o que o LuizAquino já disse, mas de uma forma mais automática.Nem é preciso pensar muito!


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)