 por TiagoFERD » Qui Mar 08, 2012 18:24
por TiagoFERD » Qui Mar 08, 2012 18:24
Boa noite!
desde já fico muito agradecido pela ajuda no tópico sobre indução que com a ajuda de vocês consegui resolve lo!
tenho uma duvida em um exercicio sobre sucessoes.
Prova que a sucessão é decrescente.
fiz se
Un+1 < Un
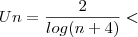

==> log(n+4) > log(n+3) ==> n+4 > n+3 ==> que é crescente.[/tex]
no livro diz que é decrescente...
Obrigado!
-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qui Mar 08, 2012 19:06
por MarceloFantini » Qui Mar 08, 2012 19:06
O termo geral é

?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por TiagoFERD » Qui Mar 08, 2012 19:21
por TiagoFERD » Qui Mar 08, 2012 19:21
MarceloFantini escreveu:O termo geral é

?
boas
não.
o Un é o

-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Qui Mar 08, 2012 19:35
por fraol » Qui Mar 08, 2012 19:35
o Un é o

A sucessão é decrescente pois o termo geral decresce, o seu raciocínio inicial estava no caminho,
você deduziu que
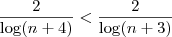
e agora?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por TiagoFERD » Qui Mar 08, 2012 19:40
por TiagoFERD » Qui Mar 08, 2012 19:40
fraol escreveu:o Un é o

A sucessão é decrescente pois o termo geral decresce, o seu raciocínio inicial estava no caminho,
você deduziu que
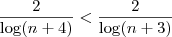
e agora?
ja percebi! foi o modo em que o livro aprensentou o resultado e estou um pouco cansado

-
TiagoFERD
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Dom Out 23, 2011 04:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por fraol » Qui Mar 08, 2012 19:47
por fraol » Qui Mar 08, 2012 19:47
Ok TiagoFERD.
MarceloFantini,
Para mostrar que a sucessão é decrescente acho que pode-se usar o raciocínio inicial do TiagoFERD.
Para provar, estava pensando em indução, você tem alguma outra dica?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Sex Mar 09, 2012 01:34
por MarceloFantini » Sex Mar 09, 2012 01:34
Acredito que ele tenha feito o raciocínio inverso. Sabemos que

, daí

, segue

e
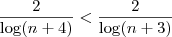
. Ele partiu da conclusão para chegar em outra coisa óbvia.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Sequências
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sucessão (Verdadeiro ou Falso)
por cardosor23 » Ter Mai 22, 2012 09:27
- 1 Respostas
- 1380 Exibições
- Última mensagem por fraol

Sáb Mai 26, 2012 01:29
Sequências
-
- Monotonia -n
por Vife » Sáb Dez 13, 2014 07:20
- 6 Respostas
- 5639 Exibições
- Última mensagem por adauto martins

Sáb Dez 13, 2014 14:25
Sequências
-
- [Sucessão e Série de funções] Convergência
por Bravim » Sex Mar 21, 2014 20:10
- 0 Respostas
- 1423 Exibições
- Última mensagem por Bravim

Sex Mar 21, 2014 20:10
Progressões
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:17
- 2 Respostas
- 2090 Exibições
- Última mensagem por adauto martins

Qui Dez 18, 2014 11:43
Geometria Analítica
-
- Estudo de reta e estudo do plano
por Livingstone » Sex Dez 12, 2014 15:21
- 0 Respostas
- 1358 Exibições
- Última mensagem por Livingstone

Sex Dez 12, 2014 15:21
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
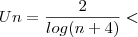
 ==> log(n+4) > log(n+3) ==> n+4 > n+3 ==> que é crescente.[/tex]
==> log(n+4) > log(n+3) ==> n+4 > n+3 ==> que é crescente.[/tex]

 ?
?


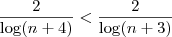

 , daí
, daí  , segue
, segue  e
e  .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
