[trigonometria]Regra de sinais

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[trigonometria]Regra de sinais

Regras do fórum
Responder

[trigonometria]Regra de sinais

Mensagempor samra » Qua Mar 07, 2012 11:33

Pergunta: Determinar o sinal do produto
P=sen56°. cos123°.sen199°.cos301°

Resolução:
Os arcos trigonométricos de medidas 56°, 123°, 199° e 301° tem extremidades no 1º,2º,3° e 4° quadrantes, respectivamente. Logo, da variação dos sinais do seno e do cosseno na circunferência trigonométrica, temos:
sen56°>0; cos123°<0; sen199°<0 e cos 301° >0
Logo, pela regra de sinais concluímos que p>0.

A QUE REGRA DE SINAIS O AUTOR DA RESOLUÇÃO SE REFERE?
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
samra
Usuário Dedicado
Usuário Dedicado
 
Mensagens: 41
Registrado em: Sex Jan 27, 2012 11:31
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Técnico em Informatica
Andamento: formado
Voltar ao topo

Re: [trigonometria]Regra de sinais

Mensagempor LuizAquino » Qua Mar 07, 2012 12:24

samra escreveu:Pergunta: Determinar o sinal do produto
P=sen56°. cos123°.sen199°.cos301°

Resolução:
Os arcos trigonométricos de medidas 56°, 123°, 199° e 301° tem extremidades no 1º,2º,3° e 4° quadrantes, respectivamente. Logo, da variação dos sinais do seno e do cosseno na circunferência trigonométrica, temos:
sen56°>0; cos123°<0; sen199°<0 e cos 301° >0
Logo, pela regra de sinais concluímos que p>0.

A QUE REGRA DE SINAIS O AUTOR DA RESOLUÇÃO SE REFERE?


Nesse contexto, "Regra de Sinais" é o mesmo que "Jogo de Sinais":

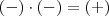
(+)\cdot (+) = (+)

(+)\cdot (-) = (-)

(-)\cdot (-) = (+)
professoraquino.com.br | youtube.com/LCMAquino | @lcmaquino

"Sem esforço, não há ganho."
Dito popular.
Avatar do usuário
LuizAquino
Colaborador Moderador - Professor
Colaborador Moderador - Professor
 
Mensagens: 2654
Registrado em: Sex Jan 21, 2011 09:11
Localização: Teófilo Otoni - MG
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Mestrado - Modelagem Computacional
Andamento: formado
Voltar ao topo
Responder

Voltar para Trigonometria

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: cálculo de limites
Autor: Hansegon - Seg Ago 25, 2008 11:29

Bom dia.

Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado

\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]

Assunto: cálculo de limites
Autor: Molina - Seg Ago 25, 2008 13:25

\lim_{x\rightarrow-1} \frac{{x}^{3}+1}{{x}^{2}-1}

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.

Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo. :y:

Caso ainda não tenha dado uma :idea:, avisa que eu resolvo.

Bom estudo!

Assunto: cálculo de limites
Autor: Guill - Dom Abr 08, 2012 16:03

\lim_{x\rightarrow-1}\frac{x^3+1}{x^2-1}

\lim_{x\rightarrow-1}\frac{(x+1)(x^2-x+1)}{(x+1)(x-1)}

\lim_{x\rightarrow-1}\frac{(x^2-x+1)}{(x-1)}=\frac{-3}{2}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum