 por Ibraim » Ter Mar 06, 2012 17:19
por Ibraim » Ter Mar 06, 2012 17:19
Boa tarde pessoal. Sou novo no fórum, qualquer problema com o tópico, por favor me avisem.
Necessito integrar a função da velocidade de um corpo em um fluido viscoso. Fazendo os cáculos, chegamos na seguinte equação:

Ele chega na seguinte equação:

Porém preciso saber como ele fez isto. Se alguém puder ajudar, agradeço!
Obrigado!
-
Ibraim
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 06, 2012 17:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Mar 06, 2012 17:40
por MarceloFantini » Ter Mar 06, 2012 17:40
Aqui estão os passos:
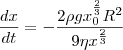
,
daí multiplique por
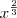
e coloque

do lado direito. Logo:
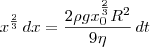
.
Basta integrar. Como no lado direito a variável t não aparece, o resto é considerado constante e é colocado fora da integral.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ibraim » Ter Mar 06, 2012 19:00
por Ibraim » Ter Mar 06, 2012 19:00
Perfeito! Consegui chegar no mesmo resultado, parecia complicado mas era simples.
Obrigado!!!
-
Ibraim
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Mar 06, 2012 17:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida - como integrar essa função?
por vinik1 » Seg Dez 05, 2011 15:53
- 2 Respostas
- 2925 Exibições
- Última mensagem por vinik1

Seg Dez 05, 2011 16:27
Cálculo: Limites, Derivadas e Integrais
-
- Como integrar essa derivada: ?2/(3x²+2)dx
por Therodrigou » Ter Set 18, 2018 03:08
- 3 Respostas
- 7970 Exibições
- Última mensagem por Gebe

Ter Set 18, 2018 15:36
Cálculo: Limites, Derivadas e Integrais
-
- Como derivar esta função: (x^3 + 7x^2 -8).(2x^-3 + x^-4)
 por fabio carvalho » Dom Mai 29, 2016 01:50
por fabio carvalho » Dom Mai 29, 2016 01:50
- 1 Respostas
- 2791 Exibições
- Última mensagem por nakagumahissao

Dom Mai 29, 2016 21:43
Cálculo: Limites, Derivadas e Integrais
-
- Como faço pra descobrir esta função e o seu grau?
por Ronaldobb » Qua Set 19, 2012 15:07
- 1 Respostas
- 1978 Exibições
- Última mensagem por MarceloFantini

Qua Set 19, 2012 22:47
Funções
-
- Como resolver esta indeterminação?
por joaofonseca » Qui Mar 22, 2012 14:57
- 2 Respostas
- 3466 Exibições
- Última mensagem por joaofonseca

Qui Mar 22, 2012 18:37
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






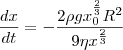 ,
,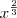 e coloque
e coloque  do lado direito. Logo:
do lado direito. Logo: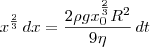 .
.



 .
.
 :
: