 por ViniRFB » Ter Mar 06, 2012 15:22
por ViniRFB » Ter Mar 06, 2012 15:22
Olá.
Queria saber uma parte de uma resolução do seguinte logaritmo. Considerando o número 4 abaixo como base, pois não sei a fórmula de base aqui.
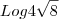
por que o resultado é:

Na parte final da resolução que tenho fica assim:
2x =

logo x =

é multiplicado apenas os denominadores? Se sim, por quê?
Desde já agradeço.
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Ter Mar 06, 2012 15:34
por ViniRFB » Ter Mar 06, 2012 15:34
Mais uma dúvida.

=

Por que o resulta não é este:
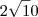
40 decomposto será 40/2=20/2=10/2=5/5=1 então o conjunto de 2 que deu 3 sairia o casal de 2, correto? logo sobrou nessa fatoração 2.5 = 10, por isso não entendi o 4 fora do radical!
Grato
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Ter Mar 06, 2012 15:42
por ViniRFB » Ter Mar 06, 2012 15:42
Sinceramente mais essa que não entendi.
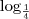
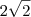
Lembrando: que

é a base, pois não sei usar a base aqui nesse sistema latex

resultado deu:
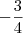
Poderia alguém me dar o passo a passo dessa?
Valeu
ViniRFB
Editado pela última vez por
ViniRFB em Ter Mar 06, 2012 17:32, em um total de 1 vez.
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Ter Mar 06, 2012 16:01
por MarceloFantini » Ter Mar 06, 2012 16:01
Sobre o primeiro, temos
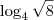
. Lembrando que
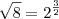
teremos
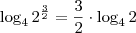
. Agora lembre-se que

, daí

.
Sobre

, quem disse que o valor é
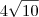
está
errado, o que você disse está correto. A resposta é
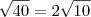
.
Tente fazer a última usando o mesmo método que fiz a primeira.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Mar 06, 2012 16:10
por LuizAquino » Ter Mar 06, 2012 16:10
ViniRFB escreveu:Considerando o número 4 abaixo como base, pois não sei a fórmula de base aqui.
(...)
Lembrando: que

é a base, pois não sei usar a base aqui nesse sistema latex

Use o carácter de "sublinhado" (ou seja, "_"). Sendo que você deve colocar entre chaves (ou seja, "{ }") a expressão desejada.
Por exemplo, observe o código:
- Código: Selecionar todos
[tex]\log_{4} \sqrt{8}[/tex]
O resultado desse código é:

ViniRFB escreveu: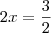
logo

é multiplicado apenas os denominadores? Se sim, por quê?
O que acontece se você dividir toda a equação por 2? Observe que:
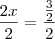
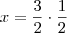
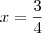
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por ViniRFB » Ter Mar 06, 2012 16:20
por ViniRFB » Ter Mar 06, 2012 16:20
LuizAquino escreveu:ViniRFB escreveu:Considerando o número 4 abaixo como base, pois não sei a fórmula de base aqui.
(...)
Lembrando: que

é a base, pois não sei usar a base aqui nesse sistema latex

Use o carácter de "sublinhado" (ou seja, "_"). Sendo que você deve colocar entre chaves (ou seja, "{ }") a expressão desejada.
Por exemplo, observe o código:
- Código: Selecionar todos
[tex]\log_{4} \sqrt{8}[/tex]
O resultado desse código é:

ViniRFB escreveu: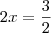
logo

é multiplicado apenas os denominadores? Se sim, por quê?
O que acontece se você dividir toda a equação por 2? Observe que:
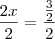
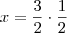
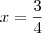
Entendi tudinho valeu a dica Aquino.
Agora estou vendo o modo que o Fantini realizou sua resolução.
Grato a todos.
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Ter Mar 06, 2012 16:29
por ViniRFB » Ter Mar 06, 2012 16:29
Sobre

, quem disse que o valor é
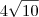
está
errado, o que você disse está correto. A resposta é
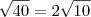
.
Sabia que estava errado. Esse é um exercício que na verdade estava pedindo o que estava certo ou errado. Agora saquei, logo entendi os conceitos.
Tente fazer a última usando o mesmo método que fiz a primeira.[/quote]
Obrigado por tudo!
ViniRFB
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Ter Mar 06, 2012 17:38
por ViniRFB » Ter Mar 06, 2012 17:38
[quote="MarceloFantini"]Sobre o primeiro, temos
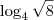
. Lembrando que
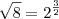
teremos
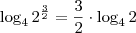
. Agora lembre-se que

, daí

.
Nessa parte não entendi

-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Ter Mar 06, 2012 17:41
por MarceloFantini » Ter Mar 06, 2012 17:41
É só lembrar que

. Escrevi na forma de fração para facilitar o entendimento que o expoente passa a multiplicar o logaritmo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Qui Mar 15, 2012 18:26
por ViniRFB » Qui Mar 15, 2012 18:26
Olá, pessoal!
Qual seria o

?
Grato
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Qui Mar 15, 2012 19:02
por MarceloFantini » Qui Mar 15, 2012 19:02
Em qual base?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por ViniRFB » Sex Mar 16, 2012 02:22
por ViniRFB » Sex Mar 16, 2012 02:22
Na verdade ví assim mesmo sema base, mas quando não tem base é 10 né? Log decimal é isso?
-
ViniRFB
- Usuário Parceiro

-
- Mensagens: 76
- Registrado em: Dom Fev 19, 2012 22:16
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2571 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1849 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Logaritmo
por JailsonJr » Sex Mai 21, 2010 05:11
- 3 Respostas
- 2733 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 17:33
Logaritmos
-
- Logaritmo (UF-CE)
por JailsonJr » Sáb Mai 22, 2010 04:56
- 6 Respostas
- 5270 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:32
Logaritmos
-
- Logaritmo
por nan_henrique » Sex Jul 09, 2010 18:38
- 1 Respostas
- 2279 Exibições
- Última mensagem por Elcioschin

Sex Jul 09, 2010 19:42
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
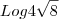 por que o resultado é:
por que o resultado é: 
 logo x =
logo x =  é multiplicado apenas os denominadores? Se sim, por quê?
é multiplicado apenas os denominadores? Se sim, por quê?

 =
= 
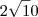
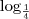
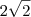
 é a base, pois não sei usar a base aqui nesse sistema latex
é a base, pois não sei usar a base aqui nesse sistema latex 
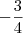
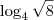 . Lembrando que
. Lembrando que 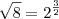 teremos
teremos 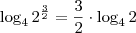 . Agora lembre-se que
. Agora lembre-se que  , daí
, daí  .
.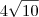 está
está 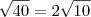 .
.


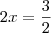 logo
logo  é multiplicado apenas os denominadores? Se sim, por quê?
é multiplicado apenas os denominadores? Se sim, por quê?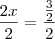
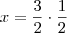
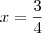
 . Escrevi na forma de fração para facilitar o entendimento que o expoente passa a multiplicar o logaritmo.
. Escrevi na forma de fração para facilitar o entendimento que o expoente passa a multiplicar o logaritmo. ?
?