Os problema são sobre séries. Os enunciados são os seguintes:
"Determine o termo geral da seguinte série: 3/2+(3*5)/(2*4)+(3*5*7)/(2*4*6)+... "
ainda não adiantei muito do problema, só cheguei ainda a uma conclusão simples, precisava de uma ajudita...
a solução deve ter por base qualquer coisa como o somatório de n=1 ate infinito dos termos dados pela expressao (2n+1)/(2n)
"Seja
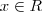 . Qual a condição necessária e suficiente sobre x para que a série
. Qual a condição necessária e suficiente sobre x para que a série 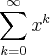 seja convergente? No caso em que a série é convergente, encontre a sua soma."
seja convergente? No caso em que a série é convergente, encontre a sua soma."Estava a pensar assumir que x deveria ser igual a 0 para a série ser convergente, mas não tenho a certeza.
Desde já obrigada a quem responder à minhas dúvidas =)


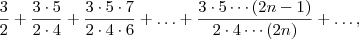



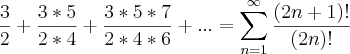 pois não?
pois não?
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.