Geometria Espacial

por **Rosana Vieira** » Sáb Mar 03, 2012 01:15

Olá estou com dúvida na resolução deste exercício
Considere um feixe de planos paralelos e duas retas que os interseccionam. Mostre que esses planos determinam, nas duas retas, segmentos proporcionais. (Um análogo ao Teorema de Tales para retas e planos no espaço).

por **timoteo** » Sáb Mar 03, 2012 15:35

primeiro temos que provar que uma reta em um feixe de paralelas é proporcional, e depois temos que provar que outra reta que tbm esteja no mesmo feixe é proporcional, utilizando o teorema de tales.

temos dois casos a considerar onde os planos tem a mesma distancia e onde os planos tem distancias diferentes. a prova que fiz foi no primeiro caso. mas, para realiza-la no segundo caso é so dividir os planos por novos planos onde a unidade entre os mesmos seja igual a u. dai fica obvio.

a segunda imagem é a primeira prova.

e a primeira imagem é a segunda prova, a legenda nao saiu entao vou coloca-la aqui.

obs: o simbolo " ~ " significa proporçao, (ainda estou aprendendo a utilizar o sistema.)

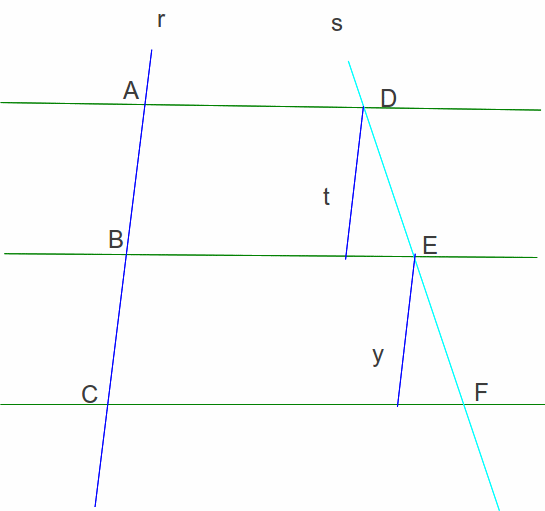
"Ficamos com t - AB e y ~ BC. Logo, t/y = AB/BC. Se observarmos que os triângulos y EF = t DE ? t/y = EF/DE, substituindo t/y = AB/BC, temos: AB/BC = EF/DE."

por **Rosana Vieira** » Sáb Mar 03, 2012 18:48

Obrigado Timoteo pela ajuda

por **Star** » Seg Mar 05, 2012 15:13

timoteo escreveu:primeiro temos que provar que uma reta em um feixe de paralelas é proporcional, e depois temos que provar que outra reta que tbm esteja no mesmo feixe é proporcional, utilizando o teorema de tales.

temos dois casos a considerar onde os planos tem a mesma distancia e onde os planos tem distancias diferentes. a prova que fiz foi no primeiro caso. mas, para realiza-la no segundo caso é so dividir os planos por novos planos onde a unidade entre os mesmos seja igual a u. dai fica obvio.

a segunda imagem é a primeira prova.

e a primeira imagem é a segunda prova, a legenda nao saiu entao vou coloca-la aqui.

obs: o simbolo " ~ " significa proporçao, (ainda estou aprendendo a utilizar o sistema.)

"Ficamos com t - AB e y ~ BC. Logo, t/y = AB/BC. Se observarmos que os triângulos y EF = t DE ? t/y = EF/DE, substituindo t/y = AB/BC, temos: AB/BC = EF/DE."

Olá Timoteo,

Não entendi o motivo de você fazer t/y = EF/DE ao envés de t/y = DE/EF e t/y = AB/BC ? DE/EF = AB/BC.

Desde já agradeço.

por **timoteo** » Seg Mar 05, 2012 19:58

Star, y EF = t DE , multiplicando y aos dois lados temos: y/y EF= t/y DE e multiplicando 1/DE aos dois membros temos: EF/DE = t/y. essas operaçoes nao atrapalham em nada a operaçao final. a segunda parte faz-se por substituiçao. afinal tudo é uma iguladade.

Star, aconselho vc a revisar as bases matematicas, eu indico os livros de Bonjorno e Castruci 5ª a 8ª.

por **Star** » Ter Mar 06, 2012 15:28

timoteo escreveu:Star, y EF = t DE , multiplicando y aos dois lados temos: y/y EF= t/y DE e multiplicando 1/DE aos dois membros temos: EF/DE = t/y. essas operaçoes nao atrapalham em nada a operaçao final. a segunda parte faz-se por substituiçao. afinal tudo é uma iguladade.

Star, aconselho vc a revisar as bases matematicas, eu indico os livros de Bonjorno e Castruci 5ª a 8ª.

Timoteo, o fato de não ter entendido o motivo de você fazer isso não tem nada a ver com o meu grau de entendimento, pois usar propriedades em razão e proporção eu sei muito bem. Você é que não entendeu que o enunciado pede que provemos que segmentos correspondentes são proporcionais e não quer que apliquemos propriedades de razão e proporção. Mas deixa pra lá você é da área de matemática aplicada e não da matemática pura este exercício é um consequência da demonstração do teorema de Tales e demonstrações precisam de rigor e objetivo e não ficar fazendo razões e proporções que são as aplicações do teorema.
Sem mais.

por **Star** » Ter Mar 06, 2012 15:51

Timóte, mas se você for um pouquinho mais humilde dê uma olhada o que o teorema de Tales diz e você vai ver que até nas propriedades de razão e proporção que você tanto "acha" que domina tem erros pois os segmentos t e DE são correspondentes e você montou a razão colocando t correspondente a EF.
http://www.brasilescola.com/matematica/teorema-tales.htm
Sem mais.

por **Star** » Ter Mar 06, 2012 15:58

E outra coisa se você usar a proporção para seguimentos correspondentes não será necessário provar para os dois casos que você cita, pois o teorema de Tales é generaliza e não supões duas situações uma onde o plano está a uma distância igual e outra em distâncias diferentes.
Sem mais.