 por Ana Carolina Caetano » Sáb Mar 03, 2012 00:13
por Ana Carolina Caetano » Sáb Mar 03, 2012 00:13
Alguem poderia me ajudar com essa questão de geometria plana? Eu tentei por P.A mas não consigo achar a razão! Desde já agradeço!
Dado um triângulo retângulo cujos catetos medem 2cm, construimos um 2º triangulo retangulo onde um dos catetos esta apoiado na hipotenusa do primeiro e o outro cateto mede 2cm. Construimos um 3º triangulo com um dos catetos medindo 2cm e o outro apoiado na hipotenusa do 2º triangulo. Se continuarmos a construir triangulos sempre da mesma forma, a hipotenusa do 15º triangulo medira:
15cm
15 raiz de 2
14 cm
8 cm (acho que é a resposta)
8 raiz de 2
-
Ana Carolina Caetano
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 02, 2012 23:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Medicina
- Andamento: cursando
 por MarceloFantini » Sáb Mar 03, 2012 00:43
por MarceloFantini » Sáb Mar 03, 2012 00:43
Não é progressão aritmética. A primeira hipotenusa tem valor
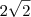
, enquanto que a segunda tem
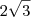
.
Repetindo a construção para o terceiro, teremos

, daí a terceira hipotenusa terá
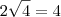
.
Novamente, para que você perceba, repetimos a construção e vemos que

, logo a quarta hipotenusa será
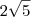
.
Consegue ver o padrão?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ana Carolina Caetano » Sáb Mar 03, 2012 01:10
por Ana Carolina Caetano » Sáb Mar 03, 2012 01:10
Entendi o padrão sim! A terceira hipotenusa é 4 e não 2 raiz de 4 certo?
Mas pra terminar o resto da questão eu vou ter que fazer até o 15º? Não tem uma forma mais rápida?
Obrigada!
-
Ana Carolina Caetano
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 02, 2012 23:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Medicina
- Andamento: cursando
 por MarceloFantini » Sáb Mar 03, 2012 01:17
por MarceloFantini » Sáb Mar 03, 2012 01:17
Bom, pela pergunta mostra que não percebeu. Lembre-se que

logo

, é uma forma diferente de escrever o mesmo número.
O padrão é, se estivermos na

-ésima construção, a hipotenusa será
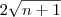
.
Primeira construção, hipotenusa:
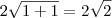
.
Segunda construção, hipotenusa:
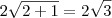
.
Terceira construção, hipotenusa:

.
Quarta construção, hipotenusa:

.
Assim em diante. Usando isso, resolva.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ana Carolina Caetano » Sáb Mar 03, 2012 01:26
por Ana Carolina Caetano » Sáb Mar 03, 2012 01:26
Ah, agora consegui! Brigadão
-
Ana Carolina Caetano
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Mar 02, 2012 23:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Medicina
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema envolvendo geometria
por Carlos28 » Sex Mai 09, 2014 21:46
- 1 Respostas
- 1369 Exibições
- Última mensagem por young_jedi

Sex Mai 09, 2014 22:15
Geometria Plana
-
- Problema envolvendo geometria e area!
 por bmachado » Seg Mar 05, 2012 22:55
por bmachado » Seg Mar 05, 2012 22:55
- 4 Respostas
- 4126 Exibições
- Última mensagem por bmachado

Seg Mar 05, 2012 23:48
Geometria Plana
-
- Geometria Plana
por claudia » Qui Out 23, 2008 16:11
- 1 Respostas
- 8718 Exibições
- Última mensagem por admin

Ter Out 28, 2008 16:47
Geometria Plana
-
- Geometria plana
por Rayanne07 » Qua Jan 13, 2010 17:40
- 3 Respostas
- 4702 Exibições
- Última mensagem por Rayanne07

Sex Jan 15, 2010 10:46
Geometria Plana
-
- Geometria Plana
 por MelvinMyster » Sex Ago 13, 2010 10:07
por MelvinMyster » Sex Ago 13, 2010 10:07
- 1 Respostas
- 4816 Exibições
- Última mensagem por alexandre32100

Sex Ago 13, 2010 13:15
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


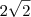 , enquanto que a segunda tem
, enquanto que a segunda tem 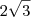 .
.  , daí a terceira hipotenusa terá
, daí a terceira hipotenusa terá 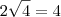 .
.  , logo a quarta hipotenusa será
, logo a quarta hipotenusa será 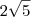 .
.

 logo
logo  , é uma forma diferente de escrever o mesmo número.
, é uma forma diferente de escrever o mesmo número. -ésima construção, a hipotenusa será
-ésima construção, a hipotenusa será 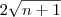 .
.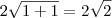 .
.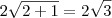 .
. .
. .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.