Alguem poderia me ajudar com essa questão de geometria plana? Eu tentei por P.A mas não consigo achar a razão! Desde já agradeço!
Dado um triângulo retângulo cujos catetos medem 2cm, construimos um 2º triangulo retangulo onde um dos catetos esta apoiado na hipotenusa do primeiro e o outro cateto mede 2cm. Construimos um 3º triangulo com um dos catetos medindo 2cm e o outro apoiado na hipotenusa do 2º triangulo. Se continuarmos a construir triangulos sempre da mesma forma, a hipotenusa do 15º triangulo medira:
15cm
15 raiz de 2
14 cm
8 cm (acho que é a resposta)
8 raiz de 2


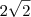 , enquanto que a segunda tem
, enquanto que a segunda tem 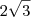 .
.  , daí a terceira hipotenusa terá
, daí a terceira hipotenusa terá 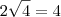 .
.  , logo a quarta hipotenusa será
, logo a quarta hipotenusa será 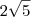 .
.

 logo
logo  , é uma forma diferente de escrever o mesmo número.
, é uma forma diferente de escrever o mesmo número. -ésima construção, a hipotenusa será
-ésima construção, a hipotenusa será 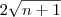 .
.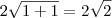 .
.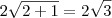 .
. .
. .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
