 por lieberth » Ter Jun 09, 2009 19:01
por lieberth » Ter Jun 09, 2009 19:01
boa tarde!!!!
estou com uma dúvida sobre pontencia!
é simples mas nao sei o que fazer 1°.
ex: 1°=14 com o expoente 2°=14 que também está com um exponte 3°=14...
1°=BASE , 2°= expoente da BASE , 3° expoente do 2° exponte da BASE
DEVO MULTIPLICAR O 14 (14X) E DEPOIS MULTIPLICAR A BASE (RESULTADO DO 14X)

NAO CONSEGUI FAZER A FÓRMULA.
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Ter Jun 09, 2009 19:47
por Cleyson007 » Ter Jun 09, 2009 19:47
Olá Lieberth!
Primeiramente, seja bem vindo ao Ajuda Matemática!
Não está dando para entender o que você está querendo dizer, mas acho que sua dúvida é a seguinte:
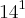



(Note que multiplica-se os expoentes).
--> A fim de ficar facilitar, repita sua pergunta usando o "Editor de Fórmulas", ok?
Um abraço.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por ginrj » Qua Jun 10, 2009 16:31
por ginrj » Qua Jun 10, 2009 16:31
acredito que seja isso mesmo que ele perguntou, tbm nao compreendi a duvida dele
Os números governam o Universo
-
ginrj
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Sex Mar 06, 2009 18:28
- Localização: Rio de Janeiro
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Pré.Militar
- Andamento: cursando
 por lieberth » Qua Jun 10, 2009 17:05
por lieberth » Qua Jun 10, 2009 17:05
obrigado pelas boas vindas.
não é isso não;
vou usar seu exemplo:
tira os parênteses e eleva o expoente 2 ao expoente 3!
é isso :
o 14 elevado a isso
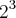
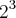
é igual 2x2x2=8
com isso ficaria

obrigado pela atenção!
-
lieberth
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Jun 09, 2009 14:57
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qua Jun 10, 2009 17:24
por Cleyson007 » Qua Jun 10, 2009 17:24
Boa tarde Lieberth!
Agora entendi o que você realmente queria (não tem os parênteses).
Sem os parênteses fica:

Da próxima vez, procure usar o "Editor de Fórmulas",

Facilita a vida de quem se dispõe a ajudá-lo.
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Vennom » Qui Fev 18, 2010 20:37
por Vennom » Qui Fev 18, 2010 20:37
Senhores, tenho um problema um tanto quanto parecido:
Qual o ultimo algarismo da potência
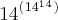
Há alguma regra que eu deva me informar a respeito?
Eu não vou postar minhas tentativas, pois não sei como tentar...
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Rodrigo Tomaz » Sáb Fev 20, 2010 14:53
por Rodrigo Tomaz » Sáb Fev 20, 2010 14:53
Boa tarde Vennom!
Eu acho o seguinte:
Como o número em questão é

, então, os últimos algarismos sempre serão 4 ou 6.
4*4=1
6*4=6
4*4=25
6...
Talvez isso você já saiba, mas o que resolverá a questão é descobrir um ritmo q isso acontece.
O último algarismo "quatro" aparece nas potências de expoentes ímpares e o último algarismo "seis" quando o expoente for par.
Então como se trata de um número elevado a uma potência 14 esse primeiro expoente é par o número ficará assim:
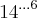
mas agora esse mesmo número se tronou um expoente da base real e sendo ele também par o número final será assim: ...
6Acho que é assim
Espero ter te ajudado!
-
Rodrigo Tomaz
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Fev 19, 2010 10:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: técnico mecânica
- Andamento: cursando
 por Vennom » Sáb Fev 20, 2010 19:57
por Vennom » Sáb Fev 20, 2010 19:57
Rodrigo Tomaz escreveu:Boa tarde Vennom!
Eu acho o seguinte:
Como o número em questão é

, então, os últimos algarismos sempre serão 4 ou 6.
4*4=1
6*4=6
4*4=25
6...
Talvez isso você já saiba, mas o que resolverá a questão é descobrir um ritmo q isso acontece.
O último algarismo "quatro" aparece nas potências de expoentes ímpares e o último algarismo "seis" quando o expoente for par.
Então como se trata de um número elevado a uma potência 14 esse primeiro expoente é par o número ficará assim:
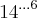
mas agora esse mesmo número se tronou um expoente da base real e sendo ele também par o número final será assim: ...
6Acho que é assim
Espero ter te ajudado!
Rodrigo, eu usei essa linha de raciocínio e aparentemente deu certo. Apesar disso, não sei se estamos pensando da forma certa. Obrigado pela ajuda. Voltar a estudar por conta própria 5 anos depois de ter terminado o ensino médio p/ prestar vestibular pode se mostrar uma tarefa não tão fácil xD .
Atenciosamente, Rafael.
-
Vennom
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Fev 18, 2010 20:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
-
- Potência de potência... não sei ao certo se entendi...
por Vennom » Sáb Fev 20, 2010 10:42
- 3 Respostas
- 3770 Exibições
- Última mensagem por mottasky

Ter Out 04, 2011 02:03
Álgebra Elementar
-
- [Potencia] soma de potencia com letras
por carla villela » Qui Mar 01, 2012 21:04
- 8 Respostas
- 8609 Exibições
- Última mensagem por carla villela

Qui Mar 01, 2012 22:18
Sistemas de Equações
-
- Potenciação - Potência de potência
por Ana Paula MMS » Sáb Jan 11, 2014 14:59
- 1 Respostas
- 2631 Exibições
- Última mensagem por Cleyson007

Sáb Jan 11, 2014 17:27
Aritmética
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2038 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



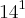


 (Note que multiplica-se os expoentes).
(Note que multiplica-se os expoentes).


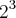



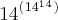
 , então, os últimos algarismos sempre serão 4 ou 6.
, então, os últimos algarismos sempre serão 4 ou 6.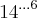 mas agora esse mesmo número se tronou um expoente da base real e sendo ele também par o número final será assim: ...
mas agora esse mesmo número se tronou um expoente da base real e sendo ele também par o número final será assim: ...
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.