 por alfabeta » Qua Fev 29, 2012 23:52
por alfabeta » Qua Fev 29, 2012 23:52
Na figura a seguir ABCD é um quadrado e TDCQ um trapézio isósceles inscrito em uma circunferência (l) de raio igual a
raiz de5 / 2 cm. Os segmentos de reta AT e BQ são tangentes à circunferência (l) em T e Q. Sabendo-se que AT e BQ têm
comprimento igual ao dobro do lado do quadrado ABCD, determine a medida do segmento de reta AB.
resposta: raiz de 2 sobre2.
tentativa:eu traçei uma reta de A até o centro da circunferencia. Desta forma, eu disse que formou-se o triangulo isosceles ATO, sendo AT = AO = 2L. Daí aplique a propriedade de propriedade de potencia de ponto com a reta tangente AT e a secante AE (reta que sai de A passa pelo centro e vai até o ponto E que criei na circunferencia). Desta forma:
AT ao quadrado= ( 2L - R)(2L +R) Mas esta conta não dá certo
Por favor, me ajude a resolver.
Se puder , me explica também como coloco as contas direitinho, como quadrado, raiz e frações.
Agradeço antecipadamente.
-
alfabeta
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Fev 28, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Qui Mar 01, 2012 16:09
por LuizAquino » Qui Mar 01, 2012 16:09
alfabeta escreveu:Na figura a seguir ABCD é um quadrado e TDCQ um trapézio isósceles inscrito em uma circunferência (l) de raio igual a
raiz de5 / 2 cm. Os segmentos de reta AT e BQ são tangentes à circunferência (l) em T e Q. Sabendo-se que AT e BQ têm
comprimento igual ao dobro do lado do quadrado ABCD, determine a medida do segmento de reta AB.
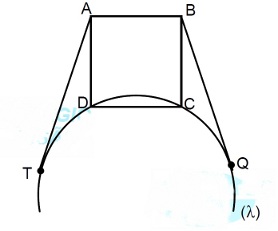
- questao 3.jpg (9.41 KiB) Exibido 1264 vezes
alfabeta escreveu:tentativa:eu traçei uma reta de A até o centro da circunferencia. Desta forma, eu disse que formou-se o triangulo isosceles ATO, sendo AT = AO = 2L. Daí aplique a propriedade de propriedade de potencia de ponto com a reta tangente AT e a secante AE (reta que sai de A passa pelo centro e vai até o ponto E que criei na circunferencia). Desta forma:
AT ao quadrado= ( 2L - R)(2L +R) Mas esta conta não dá certo
O triângulo ATO não é isósceles. Vide a figura abaixo.
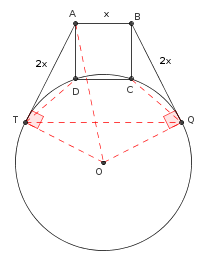
- figura1.png (6.13 KiB) Exibido 1264 vezes
Ao invés da construção que você tentou, considere a construção ilustrada na figura abaixo.
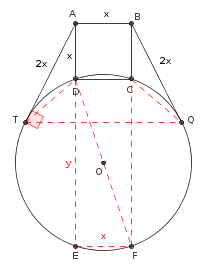
- figura2.png (6.39 KiB) Exibido 1264 vezes
Usando que DEF é um triângulo retângulo e a relação de potência entre segmento tangente e segmento secante na circunferência, temos o seguinte sistema:
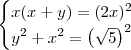
Agora basta resolver esse sistema para determinar o valor de
x.
alfabeta escreveu:Se puder , me explica também como coloco as contas direitinho, como quadrado, raiz e frações.
Por favor, vide o tópico:
DICA: Escrevendo Fórmulas com LaTeX via BBCodeviewtopic.php?f=9&t=74
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por alfabeta » Qui Mar 01, 2012 17:56
por alfabeta » Qui Mar 01, 2012 17:56
Muito obrigada!
-
alfabeta
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Ter Fev 28, 2012 11:37
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


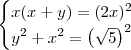



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.