 por marcia_abreu » Sáb Fev 25, 2012 18:39
por marcia_abreu » Sáb Fev 25, 2012 18:39
Por favor, preciso de ajuda com um problema de análise combinatóri?a. O problema é: Uma organização dispõe de 8 economistas e 5 engenheiros?. De quantos modos podemos formar uma comissão com 6 membros, se cada comissão deve ter, no mínimo, 3 engenheiros?? Resolvi assim: dividi a comissão de 6 membros em duas comissões de 3 membros cada uma; a primeira, uma comissão de 3 engenheiros e a segunda, uma comissão que pode ser formada com 8 economistas e os 2 engenheiros que não entraram na primeira comissão e depois multiplique?i uma pela outra para formar o número de comissões possíveis de 6 membros. Assim, na primeira comissão, são 5 engenheiros ocupando 3 lugares distintos, dividido pelo número de combinações totais de 3 engenheiros distintos, para que assim a ordem de escolha dos membros não faça diferença na comissão. Depois, a mesma coisa com os outros 10 membros (8 economistas?+2 engenheiros sobrando). A fórmula fica assim: (5x4x3/3x2) x (10x9x8/3x2?) = 1200. Mas o gabarito dá 708. Alguém pode ajudar? Grata, Marcia
-
marcia_abreu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 25, 2012 18:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História da Arte
- Andamento: formado
 por fraol » Sáb Fev 25, 2012 19:31
por fraol » Sáb Fev 25, 2012 19:31
A abordagem para resolver esse problema pode ser assim, por exemplo:
Com no mínimo 3 engenheiros em cada comissão de 6 membros, você pode ter as seguintes situações:
Uma comissão com 3 engenheiros escolhidos entre 5 e 3 economistas escolhidos entre 8:
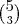
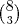
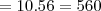
Ou
Uma comissão com 4 engenheiros escolhidos entre 5 e 2 economistas escolhidos entre 8:


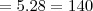
Ou
Uma comissão com 5 engenheiros escolhidos entre 5 e 1 economista escolhido entre 8:
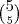
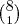
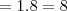
Então somando
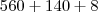
você obtém
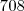
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por marcia_abreu » Sáb Fev 25, 2012 19:44
por marcia_abreu » Sáb Fev 25, 2012 19:44
Fraol, agradeço a sua ajuda. Cheguei a pensar em seguir por esse caminho tb, mas não o fiz, dá pra notar, né? Mas por favor, me diga o que há de errado com o meu raciocínio inicial. Pq a minha abordagem anterior não chega no mesmo resultado? Eu ainda não entendi qual o meu erro... Obrigada mais uma vez, Márcia
fraol escreveu:A abordagem para resolver esse problema pode ser assim, por exemplo:
Com no mínimo 3 engenheiros em cada comissão de 6 membros, você pode ter as seguintes situações:
Uma comissão com 3 engenheiros escolhidos entre 5 e 3 economistas escolhidos entre 8:
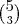
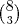
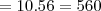
Ou
Uma comissão com 4 engenheiros escolhidos entre 5 e 2 economistas escolhidos entre 8:


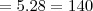
Ou
Uma comissão com 5 engenheiros escolhidos entre 5 e 1 economista escolhido entre 8:
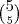
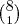
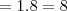
Então somando
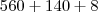
você obtém
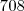
.
-
marcia_abreu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 25, 2012 18:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: História da Arte
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16390 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12560 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8482 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7935 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6631 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



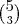
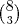
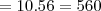


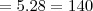
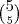
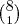
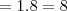
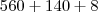 você obtém
você obtém 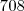 .
.
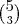
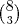


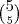
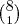
você obtém
.



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.