


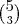
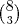
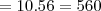


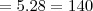
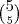
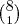
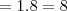
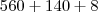 você obtém
você obtém 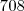 .
.
fraol escreveu:A abordagem para resolver esse problema pode ser assim, por exemplo:
Com no mínimo 3 engenheiros em cada comissão de 6 membros, você pode ter as seguintes situações:
Uma comissão com 3 engenheiros escolhidos entre 5 e 3 economistas escolhidos entre 8: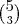
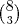
Ou
Uma comissão com 4 engenheiros escolhidos entre 5 e 2 economistas escolhidos entre 8:

Ou
Uma comissão com 5 engenheiros escolhidos entre 5 e 1 economista escolhido entre 8: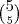
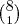
Então somandovocê obtém
.

Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.
 :
: