![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
unidades, sabendo que o eixo y contém a altura relativa ao lado AB?Eu consegui achar a altura q deu 6 unidades mas não consigo relacionar ela com a fórmula.
Desde já agradeço qualquer ajuda ou dica.

![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
unidades, sabendo que o eixo y contém a altura relativa ao lado AB?
![4.\sqrt[]{3} 4.\sqrt[]{3}](/latexrender/pictures/c0444245f15b6b85ccd929e0e777238c.png) , veremos que essa circunferência toca cada lado do triângulo, portanto esses lados são tângentes da circunferência.
, veremos que essa circunferência toca cada lado do triângulo, portanto esses lados são tângentes da circunferência.![h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2 h^2 + (2\sqrt[]{3})^2 = (4\sqrt[]{3})^2](/latexrender/pictures/d3ea7129b6d43fd44b0f7baea8bf9b5a.png)
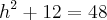


Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.