Q=QD. A tangente do ângulo CD. A tangente do ângulo CQ é:a)
![\sqrt[]{2}/4](/latexrender/pictures/bf95c6a712c75aed6a4da275fe85f94f.png "\sqrt[]{2}/4")
b)
![\sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png "\sqrt[]{2}/2")
c)
![\frac{1+\sqrt[]{2}}{2}](/latexrender/pictures/e6cfc6279c6bb115d489f73f831fbd63.png "\frac{1+\sqrt[]{2}}{2}")
d)
![\frac{\sqrt[]{2}-1}{2}](/latexrender/pictures/ebac02a4299bb17f21ab00f27de7059b.png "\frac{\sqrt[]{2}-1}{2}")
Tentativa de Resolução;
Já tentei Teorema de Pitágoras, seno, cosseno e tangente de um ângulo qualquer através da divisão do triângulo em dois outros triângulos de base 2 (metade de BC), além disso já observei as propriedades dos triângulos isósceles formados. Mas, não encontrei solução ainda.
Gabarito: A
02. (Adaptado) Nas figuras abaixo, determine o valor de x.
a) D é o ponto de encontro das 3 bissetrizes.
Tentativa de Resolução;
Busquei usar a ideia do ângulo externo ser a soma dos ângulos internos não adjacentes. Mas, os 72° dados não formam um "ângulo completo" do triângulo.
Gabarito: 18°
b)
Tentativa de Resolução;
Está descrita em vermelho na imagem.
Gabarito: 40º/3
![4.\sqrt[]{2}](/latexrender/pictures/8e5ac5085f30b7b13eb7255ae591f226.png "4.\sqrt[]{2}")
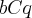é dada por:![2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png "2.\sqrt[]{2}")
![\frac{1}{2.\sqrt[]{2}} = \frac{\sqrt[]{2}}{4}](/latexrender/pictures/7de8d645671ad93c5aaac7330a7114ae.png "\frac{1}{2.\sqrt[]{2}} = \frac{\sqrt[]{2}}{4}")
por ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.