eu li sobre ele ha uns dois anos e fiquei interessado em tentar resolve-lo. pensei nele por meses sem nem colocar no papel e em uma bela noite algo me sucedeu.
nao sou um matematico, ainda, entao nao consigo concluir a prova ou sequer notar as falhas, pois estou maravilhado com a simplicidade da resposta. gostaria que vcs me ajudassem a ver algum erro ou partes confusas.
o enunciado do teorema diz: Que não há solução para a equação
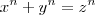 , se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0).
, se n for um inteiro maior do que 2 e x, y e z naturais (inteiros > 0).1° parte.
o enunciado diz inteiros positivos, entao sendo (a+1) a razao dos inteiros, com a > 0.
agora utilizando o binomio de Newton temos:
 para todo n
para todo n  0.
0.desenvolvendo o binomio:
 =
= 


...
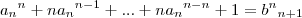
2° parte.
como podemos ver o monomio
 do primeiro termo é o antecessor de
do primeiro termo é o antecessor de 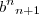 ; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n.
; esses dois termos sao valores consecutivos em uma sequencia que denominaremos de Pn para cada valor de n. sendo assim teremos para cada numero natural um conjunto de grau n. ex: P2= { 4, 9, 16...}; para cada valor natural existe um valor de grau n=2.
para encontrar dois termos consecutivos na sequencia Pn é so colocar um numero natural em
 e com isso obteremos o seu sucessor
e com isso obteremos o seu sucessor 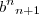 .
.3° parte.
fazendo o sucessor menos o antecessor teremos o valor
 que é a distancia entre os termos.
que é a distancia entre os termos.se observarmos as sequencias polinomiais da 1° parte perceberemos que a distancia entre os termos de grau maior n > 2 sao formados pela soma de monomios que tem expoentes n
 2.
2.o que quero provar é que o fato de a distancia entre o antecessor e sucessor é dado por um polinomio de grau n
 2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear.
2. isso para mim gera uma proporçao nao direta, diferente do que ocorre nos casos triviais de n=1 e n=2 onde a distancia é um proporçao direta formada por uma funçao linear. eu imagino que o fato de em n=2 a formula da distancia
![{D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}} {D}_{} = \sqrt[]{{(x - x)}^{2} + {(y - y)}^{2}}](/latexrender/pictures/813b779a606d9244692f21c93880efed.png) ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes n
ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes n  3 nao tem soluçao. isso prova o ultimo teorema de Fermat.
3 nao tem soluçao. isso prova o ultimo teorema de Fermat.Obs. hoje acreditam que Fermat errou ao fazer a prova, pois Sr. Wiles somente consegui a resposta utilizando matematica que nao existia no tempo de Fermat. caso essa logica esteja certa, ela pode se aproximar da resposta da epoca de Fermat.
antecipadamente agradeço as criticas construtivas.


 .
.
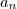 e
e 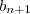 ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro
ficou confusa. Mas ao que parece, você deseja dizer que o número inteiro 
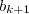 e
e 


 antes do 1, ao invés de
antes do 1, ao invés de  como deveria ser.
como deveria ser. é antecessor de
é antecessor de 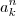 não será antecessor de
não será antecessor de 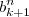 . Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².
. Por exemplo, 5 é o antecessor de 6, mas 5² não é o antecessor de 6².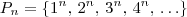
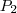 seria
seria 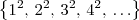 .
. seria
seria  .
. .
. ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes
ser utilizada é o fato culminante em provar que: por nao ter o mesmo comportamento as equaçoes  nao tem soluçao. isso prova o ultimo teorema de Fermat.
nao tem soluçao. isso prova o ultimo teorema de Fermat. o k-ésimo termo da sequência
o k-ésimo termo da sequência  definida anteriormente. Teremos que
definida anteriormente. Teremos que  .
.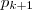 e
e 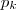 (dois termos consecutivos de
(dois termos consecutivos de 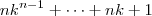 .
. .
.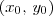 e
e  é dada por
é dada por  . Note que a expressão que você escreveu é na verdade equivalente a
. Note que a expressão que você escreveu é na verdade equivalente a 
 . usando a notaçao que vc indicou, façamos a verdadeira interpretaçao.
. usando a notaçao que vc indicou, façamos a verdadeira interpretaçao. esses dois termos estao contidos na sequencia de grau n.
esses dois termos estao contidos na sequencia de grau n.  antecessor
antecessor 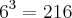 sucessor}.
sucessor}.
 .
.
 :
: