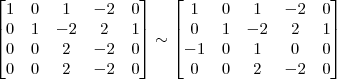
Pelo método de Gauss Jordan, agora em uma matriz de ordem 4
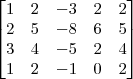

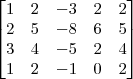


Claudin escreveu:Não consegui concluir o exercício a seguir.
Pelo método de Gauss Jordan, agora em uma matriz de ordem 4
OBS: A matriz acima já está na forma aumentada!
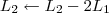
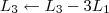

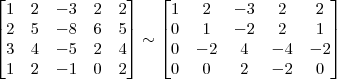

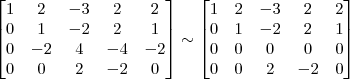

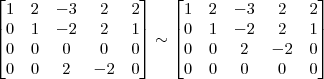
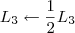
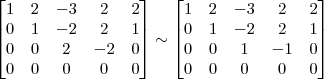
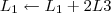
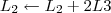
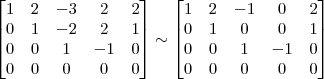
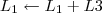
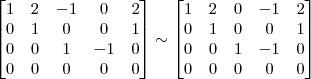
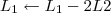
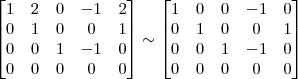
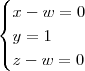

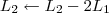
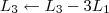

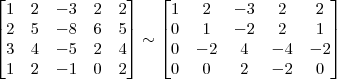

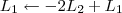
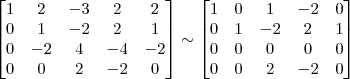
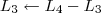
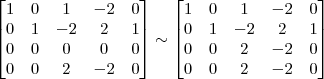

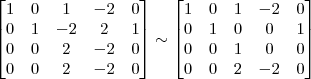
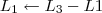
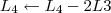
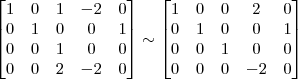
![L_4 \leftarrow [tex]\frac{-1}{2} L_4 \leftarrow [tex]\frac{-1}{2}](/latexrender/pictures/417e99a3e15d46f8753d7bb20712fc2a.png) L4[/tex]
L4[/tex]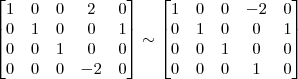
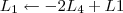
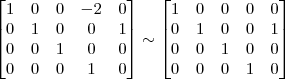
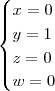

Claudin escreveu:4º Passo)
 , o resultado correto seria:
, o resultado correto seria: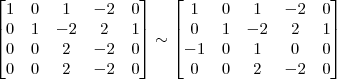

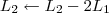
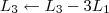

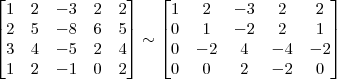

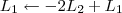
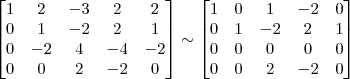
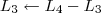
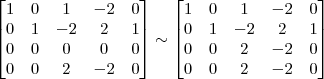

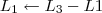
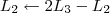
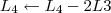
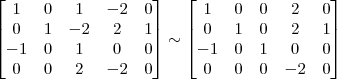
![L_4 \leftarrow [tex][tex]\frac{-1}{2}L4 L_4 \leftarrow [tex][tex]\frac{-1}{2}L4](/latexrender/pictures/59c6046357d4aab1eebeef8c0835c1e9.png)
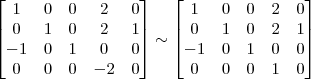
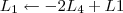
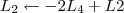
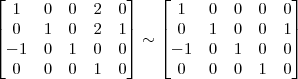

Claudin escreveu:5º Passo)
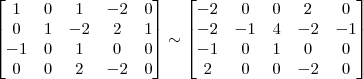



Claudin escreveu:Continuo sem compreender.
Resolvendo do jeito que eu resolvo, não consegui chegar em um resultado plausível.


Claudin escreveu:Eu resolvo do mesmo modo expresso no vídeo, transformando a diagonal principal em 1.

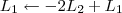
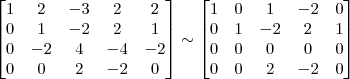

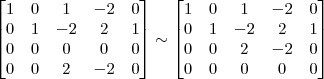
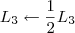
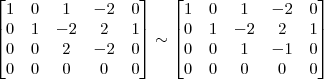
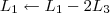
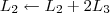
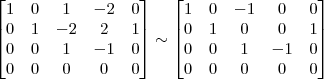
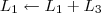
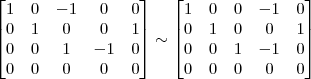
Claudin escreveu:7º Passo)
Outra dúvida, mesmo a resolução sendo errada, como ficaria representada a resposta acima, como um sistema?
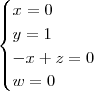


Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.