
Seja
 , calcule o valor da expressão:
, calcule o valor da expressão:
Resposta :

Comecei multiplicando (2k+1) e (2k-1) por -1, encontrando (-2k - 1) e (-2k + 1).
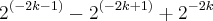
Utilizando propriedade de potência de mesma base, encontrei:
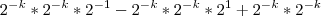
Não consegui passar disso


 , calcule o valor da expressão:
, calcule o valor da expressão:

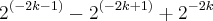
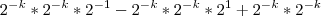

rnts escreveu:Seja, calcule o valor da expressão:
Resposta :
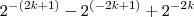
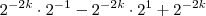
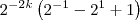
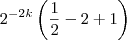
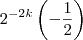
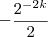

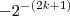

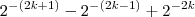

rnts escreveu:Eu olhei na apostila para ver se não tinha cometido nenhum erro, acabei não percebendo que errei. Aqui está a equação correta:
é -(2k-1) a potência do segundo 2.
 pode ser reescrito como
pode ser reescrito como  , que foi como eu escrevi em minha mensagem anterior. A resolução continua como indicado anteriormente.
, que foi como eu escrevi em minha mensagem anterior. A resolução continua como indicado anteriormente.
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)