 por nathyn » Sex Fev 10, 2012 15:21
por nathyn » Sex Fev 10, 2012 15:21
Oie, gostaria de uma ajuda pra racionalizar isso ae, por favor...
![\frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/8669a1ab7724e2db0e3c4045de7e34e1.png)
Eu já tentei fazer multiplicando por"
![\sqrt[3]{3} + 1 \sqrt[3]{3} + 1](/latexrender/pictures/405c7370a3d9db18da22f2d4fda739d8.png)
", mas não acaba não saindo da raiz nunca =/
Se puderem me ajudar... Por favor.
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Sex Fev 10, 2012 17:37
por Arkanus Darondra » Sex Fev 10, 2012 17:37
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por nathyn » Seg Fev 13, 2012 12:28
por nathyn » Seg Fev 13, 2012 12:28
Aaah entendi...
Muito obrigada =)
consegui até resolver outras questoes que eu tinha nessa mesma ideia.
Brigada mesmo =)
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Racionalização
por Rafael16 » Dom Jan 13, 2013 14:25
- 3 Respostas
- 1817 Exibições
- Última mensagem por Rafael16

Dom Jan 13, 2013 18:41
Aritmética
-
- Racionalização
 por aleson94 » Sex Mai 16, 2014 21:57
por aleson94 » Sex Mai 16, 2014 21:57
- 1 Respostas
- 1415 Exibições
- Última mensagem por Russman

Sex Mai 16, 2014 22:54
Álgebra Elementar
-
- Racionalizaçao
por Gustavo00 » Ter Mai 27, 2014 14:09
- 0 Respostas
- 1156 Exibições
- Última mensagem por Gustavo00

Ter Mai 27, 2014 14:09
Aritmética
-
- Racionalização
por Cristina Lins » Qua Abr 05, 2017 16:52
- 0 Respostas
- 1259 Exibições
- Última mensagem por Cristina Lins

Qua Abr 05, 2017 16:52
Aritmética
-
- Racionalização
por luceliasa » Sáb Jul 29, 2017 18:36
- 1 Respostas
- 2077 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 12, 2017 19:07
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/8669a1ab7724e2db0e3c4045de7e34e1.png)
![\sqrt[3]{3} + 1 \sqrt[3]{3} + 1](/latexrender/pictures/405c7370a3d9db18da22f2d4fda739d8.png) ", mas não acaba não saindo da raiz nunca =/
", mas não acaba não saindo da raiz nunca =/
![\frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/8669a1ab7724e2db0e3c4045de7e34e1.png)
![\sqrt[3]{3} + 1 \sqrt[3]{3} + 1](/latexrender/pictures/405c7370a3d9db18da22f2d4fda739d8.png) ", mas não acaba não saindo da raiz nunca =/
", mas não acaba não saindo da raiz nunca =/
![\frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/8669a1ab7724e2db0e3c4045de7e34e1.png)
![\frac{\sqrt[3]{3^2} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{3^2} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/2c75ec31a5b9d49a67352873e05df717.png)
![\frac{(\sqrt[3]{3})^2 - 1^2}{\sqrt[3]{3} - 1} \frac{(\sqrt[3]{3})^2 - 1^2}{\sqrt[3]{3} - 1}](/latexrender/pictures/8421c1c4fed643e26571b25bba2736aa.png)
![\frac{(\sqrt[3]{3}-1)(\sqrt[3]{3}+1)}{\sqrt[3]{3} - 1)} \frac{(\sqrt[3]{3}-1)(\sqrt[3]{3}+1)}{\sqrt[3]{3} - 1)}](/latexrender/pictures/1616fb5a8e597bae91331abd3e8cb09b.png)
![\sqrt[3]{3}+1 \sqrt[3]{3}+1](/latexrender/pictures/33f866ece40e94444ed1b35fd00951b8.png)
", mas não acaba não saindo da raiz nunca =/
![\sqrt[3]{3}.\sqrt[3]{3^2} = \sqrt[3]{3^3} = 3 \sqrt[3]{3}.\sqrt[3]{3^2} = \sqrt[3]{3^3} = 3](/latexrender/pictures/8a66e10a85cd28812c9e6866a232e59f.png)
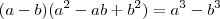
![\frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1} \frac{\sqrt[3]{9} - 1}{\sqrt[3]{3} - 1}](/latexrender/pictures/8669a1ab7724e2db0e3c4045de7e34e1.png)
![\frac{\sqrt[3]{3^2}-1^2}{\sqrt[3]{3}-1}.\frac{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2} \frac{\sqrt[3]{3^2}-1^2}{\sqrt[3]{3}-1}.\frac{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}](/latexrender/pictures/d2bf3a4c6288d68f16730b766ac13afb.png)
![\frac{(\sqrt[3]{3}+1)(\sqrt[3]{3}-1^3)}{\sqrt[3]{3}-1^3}.\frac{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2} \frac{(\sqrt[3]{3}+1)(\sqrt[3]{3}-1^3)}{\sqrt[3]{3}-1^3}.\frac{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}{\sqrt[3]{3^2}+\sqrt[3]{3}.1+1^2}](/latexrender/pictures/b874db8f1c61ef333eecc47a5bcb083c.png)
![\frac{(\sqrt[3]{3}+1)(\sqrt[3]{3^3}-1^3)}{\sqrt[3]{3^3}-1^3} \frac{(\sqrt[3]{3}+1)(\sqrt[3]{3^3}-1^3)}{\sqrt[3]{3^3}-1^3}](/latexrender/pictures/0056a657c2dec1a274753651183b7bf4.png)
![\frac{(\sqrt[3]{3}+1)(3-1)}{3-1} \frac{(\sqrt[3]{3}+1)(3-1)}{3-1}](/latexrender/pictures/2cf509fd62ba83810ac5e1fd982a7249.png)
![\sqrt[3]{3}+1 \sqrt[3]{3}+1](/latexrender/pictures/33f866ece40e94444ed1b35fd00951b8.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
