Racionalize :
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}}](/latexrender/pictures/25a9e31131bd6bcd8630859d3700aeab.png)
Tentei fazer como se fosse uma diferença de quadrados assim :
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}](/latexrender/pictures/8e1f878d4a0af5bdc55f8ba13d98a3c5.png)
Mas acho que está errado, não consegui fazer a partir daí.
Resposta :
![\frac{1+\sqrt[]{2}-\sqrt[]{3}}{4} \frac{1+\sqrt[]{2}-\sqrt[]{3}}{4}](/latexrender/pictures/e1ef3cd6193818cd397bb3e9ed4a0762.png)
2)
![\left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2} \left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2}](/latexrender/pictures/59f9cb9406acf6b9e468eb00d66bf571.png)
Tentei racionalizar a expressão com a forma fatorada do numerador :
![\frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}} \frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}}](/latexrender/pictures/e3c5be7753d74ebecd0d25e9df577f98.png)
Mas o resultado deu outra maçaroca
Resposta
![2\sqrt[6]{2} 2\sqrt[6]{2}](/latexrender/pictures/a4392559fde94680c9899b9979020815.png)
3)
![\sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/efb31d2e63572cf7b8e849433cad3cba.png)
tentei aplicar distributiva(não sei nem se isso é permitido nessa expressão) mas não cheguei a lugar algum.
Reposta :
![-\sqrt[3]{3} -\sqrt[3]{3}](/latexrender/pictures/c2d7a58884f31156806122116bd7d291.png)
4)Determine o nº a que satisfaz a expressão:
![\frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2} \frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2}](/latexrender/pictures/6c9b6466a6ebae34f16719210cc7bd51.png)
Nessa eu não faço a menor idéia de como proceder
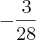
5)
![\frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1} \frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1}](/latexrender/pictures/285399e20655ec09bc3ca9934ec29351.png)
Tbm não destrinchei
Resultado : 4
6)
![{\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8} {\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8}](/latexrender/pictures/0692dc2c36b12339629e6b902e20d85b.png)
Nesta eu tentei fazer o seguinte :
![\sqrt[6]{2\sqrt[]{{2}^{8}}} \sqrt[6]{2\sqrt[]{{2}^{8}}}](/latexrender/pictures/8d8f66dd48aa42e230f117df3519d6c5.png)
=
![\sqrt[6]{2\sqrt[]{256}} \sqrt[6]{2\sqrt[]{256}}](/latexrender/pictures/69dc03384eff080804cec837e0f696f1.png) =
= ![\sqrt[6]{2.16}} \sqrt[6]{2.16}}](/latexrender/pictures/aef9d963797f2c0525c88fe710589d42.png) =
= ![\sqrt[6]{32}} \sqrt[6]{32}}](/latexrender/pictures/610b33cb1a3ceb3db2478e7cbe2e7daa.png)
E trava aí
A resposta desse exercício é 4



![\frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]} \frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]}](/latexrender/pictures/a1da94a6662b824ee7b20aef7ac1486e.png)
![\left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2} \left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2}](/latexrender/pictures/56fa34c5579cb1067d0e39ad33c2f595.png)
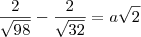
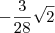 . Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer
. Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer 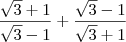
![\frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)} \frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)}](/latexrender/pictures/7a26acdeb571fa620321f92c9349dc63.png)
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8}](/latexrender/pictures/9ddb77297864b8604e49544f1b7f3661.png)
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8}](/latexrender/pictures/3011483466e67a9aba92bd43d1f6ee90.png)
![\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}](/latexrender/pictures/47ecf4ba0fd97ee371ef049103704726.png)

![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png) se transformou em
se transformou em ![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png)

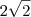 se transformou em
se transformou em 
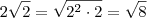


![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}}](/latexrender/pictures/6eeac228cfa7f26c6734250aeccda2bb.png)
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6}](/latexrender/pictures/7e27ed046007354431fe2dd456416935.png)
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/cac9a3798f1b94319c235b7f8cfb6e8a.png)
![\frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8} \frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8}](/latexrender/pictures/b718adb676d85bd6a07de8227a184f2c.png)
![\frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8} \frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8}](/latexrender/pictures/0e5bdd978030cae907a3e02b0030ab84.png)
![\frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4} \frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4}](/latexrender/pictures/3454c7f7d32112ae8d1ac43ee1530022.png)
![\frac{1\sqrt[]{2} +\sqrt[]{3}}{4} \frac{1\sqrt[]{2} +\sqrt[]{3}}{4}](/latexrender/pictures/d5a98b1546baaf13361a9b667131bd8a.png)
![\frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}} \frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}}](/latexrender/pictures/2fe825db061b644fcd2f356f18281527.png)
![\left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right) \left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right)](/latexrender/pictures/0093ba7dd8b9eff58a02eeb302c78d8d.png)
![\left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right) \left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right)](/latexrender/pictures/926aded02e900b2d0046c389e539665c.png)





![\frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}} \frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}}](/latexrender/pictures/936249e25498e25ffbc85ec40ccf9e85.png)
![\left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right) \left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right)](/latexrender/pictures/f39a8b6cf602d2758e5f7b757e9479a1.png)
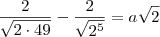

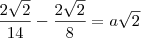


![=\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2} =\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2}](/latexrender/pictures/b62ef232b3674806c0f276037e45d7fb.png)
![\left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right) \left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right)](/latexrender/pictures/603e6c34ffaaf530b8bc4084fa9166d8.png)
![3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9} 3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9}](/latexrender/pictures/1fd2549717861a7aee748b413dbf44ba.png)
![+5\sqrt[3]{3}-6\sqrt[3]{3} +5\sqrt[3]{3}-6\sqrt[3]{3}](/latexrender/pictures/2817cd9c822e3020313b94124bf7bf22.png)
![\frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1} \frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1}](/latexrender/pictures/9978dfe8da24d6a95f69665fbe2efc91.png)
![\frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2} \frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2}](/latexrender/pictures/e9f3f7b194d0c196123ade0305daab6a.png)
 =
= 
![-5\sqrt[3]{3} -5\sqrt[3]{3}](/latexrender/pictures/f482f41c1d4790fa1a76fe2473035097.png) e não
e não ![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png) como você escreveu.
como você escreveu.![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/a329addd67fe6089d0876a9c982c0330.png) é equivalente a
é equivalente a ![-11\sqrt[3]{3} -11\sqrt[3]{3}](/latexrender/pictures/10a3a4eb8435cdf802dcd3336b920906.png) .
.![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/1b7856884e6cd6ce09155ac944ea401e.png) é equivalente a
é equivalente a 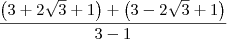
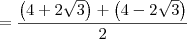



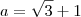 e
e 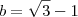 .
.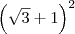 ;
;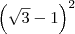 ;
;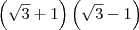 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)