 por Andrewo » Qua Fev 01, 2012 13:43
por Andrewo » Qua Fev 01, 2012 13:43
Dae galerê, de novo c radicais, é chato mas eu não posso deixar passar , pq se eu não for capaz de resolver uma quantidade grande de exercícios de um só assunto ,penso que não adianta nada.
Racionalize :
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}}](/latexrender/pictures/25a9e31131bd6bcd8630859d3700aeab.png)
Tentei fazer como se fosse uma diferença de quadrados assim :
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}](/latexrender/pictures/8e1f878d4a0af5bdc55f8ba13d98a3c5.png)
Mas acho que está errado, não consegui fazer a partir daí.
Resposta :
![\frac{1+\sqrt[]{2}-\sqrt[]{3}}{4} \frac{1+\sqrt[]{2}-\sqrt[]{3}}{4}](/latexrender/pictures/e1ef3cd6193818cd397bb3e9ed4a0762.png)
2)
![\left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2} \left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2}](/latexrender/pictures/59f9cb9406acf6b9e468eb00d66bf571.png)
Tentei racionalizar a expressão com a forma fatorada do numerador :
![\frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}} \frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}}](/latexrender/pictures/e3c5be7753d74ebecd0d25e9df577f98.png)
Mas o resultado deu outra maçaroca
Resposta
![2\sqrt[6]{2} 2\sqrt[6]{2}](/latexrender/pictures/a4392559fde94680c9899b9979020815.png)
3)
![\sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/efb31d2e63572cf7b8e849433cad3cba.png)
tentei aplicar distributiva(não sei nem se isso é permitido nessa expressão) mas não cheguei a lugar algum.
Reposta :
![-\sqrt[3]{3} -\sqrt[3]{3}](/latexrender/pictures/c2d7a58884f31156806122116bd7d291.png)
4)Determine o nº a que satisfaz a expressão:
![\frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2} \frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2}](/latexrender/pictures/6c9b6466a6ebae34f16719210cc7bd51.png)
Nessa eu não faço a menor idéia de como proceder
5)
![\frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1} \frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1}](/latexrender/pictures/285399e20655ec09bc3ca9934ec29351.png)
Tbm não destrinchei
Resultado : 4
6)
![{\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8} {\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8}](/latexrender/pictures/0692dc2c36b12339629e6b902e20d85b.png)
Nesta eu tentei fazer o seguinte :
![\sqrt[6]{2\sqrt[]{{2}^{8}}} \sqrt[6]{2\sqrt[]{{2}^{8}}}](/latexrender/pictures/8d8f66dd48aa42e230f117df3519d6c5.png)
=
![\sqrt[6]{2\sqrt[]{256}} \sqrt[6]{2\sqrt[]{256}}](/latexrender/pictures/69dc03384eff080804cec837e0f696f1.png)
=
![\sqrt[6]{2.16}} \sqrt[6]{2.16}}](/latexrender/pictures/aef9d963797f2c0525c88fe710589d42.png)
=
![\sqrt[6]{32}} \sqrt[6]{32}}](/latexrender/pictures/610b33cb1a3ceb3db2478e7cbe2e7daa.png)
E trava aí
A resposta desse exercício é 4
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Fev 01, 2012 14:20
por LuizAquino » Qua Fev 01, 2012 14:20
Andrewo escreveu:Racionalize :

Comece fazendo:
![\frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]} \frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]}](/latexrender/pictures/a1da94a6662b824ee7b20aef7ac1486e.png)
Agora tente terminar.
Andrewo escreveu:2)
![\left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2} \left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2}](/latexrender/pictures/56fa34c5579cb1067d0e39ad33c2f595.png)
Comece transformando todos os radicais para o mesmo índice 6.
Andrewo escreveu:3)
![\sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/efb31d2e63572cf7b8e849433cad3cba.png)
Comece aplicando a distributiva (como você mesmo já disse).
Andrewo escreveu:4)Determine o nº a que satisfaz a expressão:
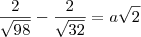
Comece racionalizando os denominadores que aparecem no lado direito. Após fazer todas as simplificações, você verá que nesse lado sobrará apenas
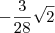
. Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer
a que aparece no lado esquerdo.
Andrewo escreveu:5)
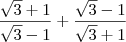
Comece efetuando a soma dessas frações. Ou seja, você terá que:
![\frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)} \frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)}](/latexrender/pictures/7a26acdeb571fa620321f92c9349dc63.png)
Andrewo escreveu:6)
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8}](/latexrender/pictures/9ddb77297864b8604e49544f1b7f3661.png)
Comece percebendo que:
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8}](/latexrender/pictures/3011483466e67a9aba92bd43d1f6ee90.png)
Em seguida, lembre-se da propriedade:
![\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}](/latexrender/pictures/47ecf4ba0fd97ee371ef049103704726.png) Observação
ObservaçãoPor questão de organização do fórum, nós recomendamos que em cada tópico haja apenas um exercício.
Além disso, vale lembrar que não é objetivo do fórum resolver listas de exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andrewo » Qui Fev 02, 2012 12:03
por Andrewo » Qui Fev 02, 2012 12:03
LuizAquino escreveu:Comece percebendo que:
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8}](/latexrender/pictures/3011483466e67a9aba92bd43d1f6ee90.png)
Em seguida, lembre-se da propriedade:
![\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}](/latexrender/pictures/47ecf4ba0fd97ee371ef049103704726.png)
Não percebo, pq o
![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png)
se transformou em
![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png)
LuizAquino escreveu:Observação
Por questão de organização do fórum, nós recomendamos que em cada tópico haja apenas um exercício.
Além disso, vale lembrar que não é objetivo do fórum resolver listas de exercício.
Minha intenção não é que façam listas de exercícios pra mim e sim aprender e tirar dúvidas.Mas de qualquer forma vou tentar limitar o máximo os problemas que eu postar aqui.

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qui Fev 02, 2012 13:42
por LuizAquino » Qui Fev 02, 2012 13:42
Andrewo escreveu:Não percebo, pq o
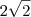
se transformou em

Note que:
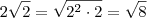
Andrewo escreveu:Minha intenção não é que façam listas de exercícios pra mim e sim aprender e tirar dúvidas. Mas de qualquer forma vou tentar limitar o máximo os problemas que eu postar aqui.
Você não precisa se preocupar em limitar o número de exercícios que você irá postar. Apenas procure enviar um exercício por tópico.
Além disso, ao enviar um exercício você pode fazer como você fez nesse tópico: indicar as suas tentativas e informar exatamente onde está a sua dúvida. Isso é muito bom, pois indica que você quer tirar dúvidas e não simplesmente ter o exercício resolvido.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Qui Fev 02, 2012 13:43
por Arkanus Darondra » Qui Fev 02, 2012 13:43
Andrewo escreveu:Não percebo, pq o
![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png)
se transformou em
![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png)
Note que

O inverso, obviamente, também é válido. Para isso, basta fatorar o 8.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Andrewo » Ter Fev 07, 2012 14:53
por Andrewo » Ter Fev 07, 2012 14:53
To com mta dificuldade nesses exercícios.
LuizAquino escreveu:Andrewo escreveu:Racionalize :

Comece fazendo:
![\frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]} \frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]}](/latexrender/pictures/a1da94a6662b824ee7b20aef7ac1486e.png)
Agora tente terminar.
Fiz essa, o resultado saiu parecido, mas não o mesmo, vejam se tá errado:
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}}](/latexrender/pictures/6eeac228cfa7f26c6734250aeccda2bb.png)
=
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6}](/latexrender/pictures/7e27ed046007354431fe2dd456416935.png)
=
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/cac9a3798f1b94319c235b7f8cfb6e8a.png)
=
![\frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8} \frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8}](/latexrender/pictures/b718adb676d85bd6a07de8227a184f2c.png)
Aqui dividi o 2 e o 8 por 2 \/
=
![\frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8} \frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8}](/latexrender/pictures/0e5bdd978030cae907a3e02b0030ab84.png)
=
![\frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4} \frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4}](/latexrender/pictures/3454c7f7d32112ae8d1ac43ee1530022.png)
o 1 aqui nao ficou somando e sim multiplicando
=
![\frac{1\sqrt[]{2} +\sqrt[]{3}}{4} \frac{1\sqrt[]{2} +\sqrt[]{3}}{4}](/latexrender/pictures/d5a98b1546baaf13361a9b667131bd8a.png)
Andrewo escreveu:2)
![\left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2} \left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2}](/latexrender/pictures/56fa34c5579cb1067d0e39ad33c2f595.png)
Comece transformando todos os radicais para o mesmo índice 6.
![\frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}} \frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}}](/latexrender/pictures/2fe825db061b644fcd2f356f18281527.png)
Mas e agora, parceiro?
Andrewo escreveu:3)
![\sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/efb31d2e63572cf7b8e849433cad3cba.png)
Comece aplicando a distributiva (como você mesmo já disse).
Bom, aplicando a distributiva deu isso:
![\left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right) \left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right)](/latexrender/pictures/0093ba7dd8b9eff58a02eeb302c78d8d.png)
=
![\left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right) \left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right)](/latexrender/pictures/926aded02e900b2d0046c389e539665c.png)
Aqui travou
Andrewo escreveu:4)Determine o nº a que satisfaz a expressão:
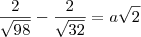
Comece racionalizando os denominadores que aparecem no lado direito. Após fazer todas as simplificações, você verá que nesse lado sobrará apenas
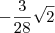
. Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer
a que aparece no lado esquerdo.
Andrewo escreveu:5)
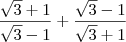
Comece efetuando a soma dessas frações. Ou seja, você terá que:
![\frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)} \frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)}](/latexrender/pictures/7a26acdeb571fa620321f92c9349dc63.png)
Essas duas contas eu tive que desistir delas :s
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Fev 07, 2012 18:28
por LuizAquino » Ter Fev 07, 2012 18:28
Andrewo escreveu:Aqui dividi o 2 e o 8 por 2 \/


Aqui está o erro.
O correto seria:




Andrewo escreveu:![\frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}} \frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}}](/latexrender/pictures/2fe825db061b644fcd2f356f18281527.png)
Mas e agora, parceiro?
Note que:
![\frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}} \frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}}](/latexrender/pictures/936249e25498e25ffbc85ec40ccf9e85.png)
Agora continue.
Andrewo escreveu:Bom, aplicando a distributiva deu isso:
![\left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right) \left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right)](/latexrender/pictures/0093ba7dd8b9eff58a02eeb302c78d8d.png)
Aqui está errado.
O correto seria:
![\left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right) \left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right)](/latexrender/pictures/f39a8b6cf602d2758e5f7b757e9479a1.png)
Tente continuar a partir daí.
Andrewo escreveu:4) Determine o nº a que satisfaz a expressão:
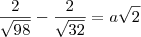
5)
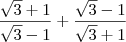
Andrewo escreveu:Essas duas contas eu tive que desistir delas :s
4) Note que:
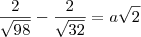
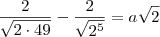

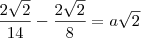

Agora tente terminar a partir daí.
5) Note que:

![=\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2} =\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2}](/latexrender/pictures/b62ef232b3674806c0f276037e45d7fb.png)
Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Andrewo » Qua Fev 08, 2012 11:44
por Andrewo » Qua Fev 08, 2012 11:44
LuizAquino escreveu:Aqui está errado.
O correto seria:
![\left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right) \left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right)](/latexrender/pictures/f39a8b6cf602d2758e5f7b757e9479a1.png)
Tente continuar a partir daí.
Nessa conta eu fiquei meio na dúvida.
![\left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right) \left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right)](/latexrender/pictures/603e6c34ffaaf530b8bc4084fa9166d8.png)
O que poderia acontecer aqui é o sinal trocar na 2º expressão?????????? e ficar então:
![3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9} 3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9}](/latexrender/pictures/1fd2549717861a7aee748b413dbf44ba.png)
![+5\sqrt[3]{3}-6\sqrt[3]{3} +5\sqrt[3]{3}-6\sqrt[3]{3}](/latexrender/pictures/2817cd9c822e3020313b94124bf7bf22.png)
![-\sqrt[3]{3} -\sqrt[3]{3}](/latexrender/pictures/c2d7a58884f31156806122116bd7d291.png)
É isso?
5) Note que:

![=\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2} =\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2}](/latexrender/pictures/b62ef232b3674806c0f276037e45d7fb.png)
Tente continuar a partir daí.
Bom, veja se tá certo.
![\frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1} \frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1}](/latexrender/pictures/9978dfe8da24d6a95f69665fbe2efc91.png)
=
![\frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2} \frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2}](/latexrender/pictures/e9f3f7b194d0c196123ade0305daab6a.png)
=

=

A minha dúvida nessa questão é :
Pq numa soma de fração os numeradores se transformaram em quadrado da soma e quadrado da diferença e o numerador numa diferença de quadrados?As outras contas eu consegui resolver
Vlwwww Aquino





-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Fev 08, 2012 12:22
por LuizAquino » Qua Fev 08, 2012 12:22
Andrewo escreveu:Nessa conta eu fiquei meio na dúvida.
![\left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right) \left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right)](/latexrender/pictures/603e6c34ffaaf530b8bc4084fa9166d8.png)
O que poderia acontecer aqui é o sinal trocar na 2º expressão?
A ideia é sim trocar o sinal. Mas confira as suas contas, pois no primeiro termo deve haver
![-5\sqrt[3]{3} -5\sqrt[3]{3}](/latexrender/pictures/f482f41c1d4790fa1a76fe2473035097.png)
e não
![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png)
como você escreveu.
Vale destacar que o valor de
![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/a329addd67fe6089d0876a9c982c0330.png)
é equivalente a
![-11\sqrt[3]{3} -11\sqrt[3]{3}](/latexrender/pictures/10a3a4eb8435cdf802dcd3336b920906.png)
.
Já o valor de
![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/1b7856884e6cd6ce09155ac944ea401e.png)
é equivalente a
![-\sqrt[3]{3} -\sqrt[3]{3}](/latexrender/pictures/c2d7a58884f31156806122116bd7d291.png)
.
Ok.
Andrewo escreveu:A minha dúvida nessa questão é : Pq numa soma de fração os numeradores se transformaram em quadrado da soma e quadrado da diferença e o numerador numa diferença de quadrados?
Isso não acontece em todas as somas de fração. Apenas nesse caso.
Imagine que você deseja calcular a soma:

Resolvendo essa soma, obtemos:

Comparando com o exercício, temos que
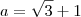
e
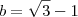
.
Temos então que:
(i) a² será equivalente ao quadrado da soma:
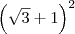
;
(ii) b² será equivalente ao quadrado da diferença:
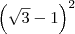
;
(iii) ab será equivalente ao produto da soma pela diferença:
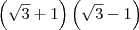
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2332 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1875 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
-
- Radicais de nv
por Andrewo » Seg Fev 13, 2012 16:58
- 4 Respostas
- 2452 Exibições
- Última mensagem por Arkanus Darondra

Ter Fev 14, 2012 13:01
Álgebra Elementar
-
- Problema com radicais
por thadeu » Ter Nov 24, 2009 20:27
- 0 Respostas
- 1011 Exibições
- Última mensagem por thadeu

Ter Nov 24, 2009 20:27
Álgebra Elementar
-
- Limite com radicais
por valeuleo » Qui Mar 31, 2011 08:46
- 3 Respostas
- 5426 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}}](/latexrender/pictures/25a9e31131bd6bcd8630859d3700aeab.png)
![\frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)} \frac{1}{2 + \sqrt[]{2} + \sqrt[]{6}} . \frac{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}{2 - \left( \sqrt[]{2} + \sqrt[]{6} \right)}](/latexrender/pictures/8e1f878d4a0af5bdc55f8ba13d98a3c5.png)
![\frac{1+\sqrt[]{2}-\sqrt[]{3}}{4} \frac{1+\sqrt[]{2}-\sqrt[]{3}}{4}](/latexrender/pictures/e1ef3cd6193818cd397bb3e9ed4a0762.png)
![\left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2} \left( 4\sqrt[]{8} - 2\sqrt[]{18} \right) : \sqrt[3]{2}](/latexrender/pictures/59f9cb9406acf6b9e468eb00d66bf571.png)
![\frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}} \frac{\left( 4.2\sqrt[]{2} - 2.3\sqrt[]{2} \right)}{\sqrt[3]{2}} . \frac{\sqrt[3]{{2}^{2}}}{\sqrt[3]{{2}^{2}}}](/latexrender/pictures/e3c5be7753d74ebecd0d25e9df577f98.png)
![2\sqrt[6]{2} 2\sqrt[6]{2}](/latexrender/pictures/a4392559fde94680c9899b9979020815.png)
![\sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}.\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}.\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/efb31d2e63572cf7b8e849433cad3cba.png)
![-\sqrt[3]{3} -\sqrt[3]{3}](/latexrender/pictures/c2d7a58884f31156806122116bd7d291.png)
![\frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2} \frac{2}{\sqrt[]{98}} - \frac{2}{\sqrt[]{32}} = a\sqrt[]{2}](/latexrender/pictures/6c9b6466a6ebae34f16719210cc7bd51.png)
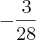
![\frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1} \frac{\sqrt[]{3}+1}{\sqrt[]{3}-1} + \frac{\sqrt[]{3}-1}{\sqrt[]{3}+1}](/latexrender/pictures/285399e20655ec09bc3ca9934ec29351.png)
![{\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8} {\left( \sqrt[]{\sqrt[3]{2\sqrt[]{2}}} \right)}^{8}](/latexrender/pictures/0692dc2c36b12339629e6b902e20d85b.png)
![\sqrt[6]{2\sqrt[]{{2}^{8}}} \sqrt[6]{2\sqrt[]{{2}^{8}}}](/latexrender/pictures/8d8f66dd48aa42e230f117df3519d6c5.png)
![\sqrt[6]{2\sqrt[]{256}} \sqrt[6]{2\sqrt[]{256}}](/latexrender/pictures/69dc03384eff080804cec837e0f696f1.png) =
= ![\sqrt[6]{2.16}} \sqrt[6]{2.16}}](/latexrender/pictures/aef9d963797f2c0525c88fe710589d42.png) =
= ![\sqrt[6]{32}} \sqrt[6]{32}}](/latexrender/pictures/610b33cb1a3ceb3db2478e7cbe2e7daa.png)



![\frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]} \frac{1}{2 + \sqrt{2} + \sqrt{6}} = \frac{1\cdot \left[\left(2+\sqrt{2} - \sqrt{6}\right)\right]}{\left[\left(2 + \sqrt{2}\right) + \sqrt{6}\right]\cdot \left[\left(2+\sqrt{2}\right) - \sqrt{6}\right]}](/latexrender/pictures/a1da94a6662b824ee7b20aef7ac1486e.png)
![\left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2} \left( 4\sqrt{8} - 2\sqrt{18} \right) : \sqrt[3]{2}](/latexrender/pictures/56fa34c5579cb1067d0e39ad33c2f595.png)
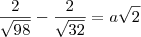
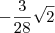 . Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer
. Se no lado direito sobrará isso, então fica fácil você deduzir quanto deve valer 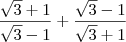
![\frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)} \frac{\sqrt{3}+1}{\sqrt{3}-1} + \frac{\sqrt{3}-1}{\sqrt{3}+1} =\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}+1\right) + \left(\sqrt{3}-1\right)\left(\sqrt{3}-1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt[]{3}+1\right)}](/latexrender/pictures/7a26acdeb571fa620321f92c9349dc63.png)
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8}](/latexrender/pictures/9ddb77297864b8604e49544f1b7f3661.png)
![{\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8} {\left(\sqrt{\sqrt[3]{2\sqrt{2}}} \right)}^{8} = {\left(\sqrt{\sqrt[3]{\sqrt{8}}} \right)}^{8}](/latexrender/pictures/3011483466e67a9aba92bd43d1f6ee90.png)
![\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} \sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}](/latexrender/pictures/47ecf4ba0fd97ee371ef049103704726.png)

![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png) se transformou em
se transformou em ![\sqrt[]{8} \sqrt[]{8}](/latexrender/pictures/32d685ae155e3c326c41fafed80cb5df.png)

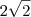 se transformou em
se transformou em 
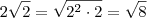


![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{{\left(2+\sqrt[]{2} \right)}^{2} - {\sqrt[]{6}}^{2}}](/latexrender/pictures/6eeac228cfa7f26c6734250aeccda2bb.png)
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{\left(4+4\sqrt[]{2}+2 \right)- 6}](/latexrender/pictures/7e27ed046007354431fe2dd456416935.png)
![\frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}} \frac{2+\sqrt[]{2}-\sqrt[]{6}}{4\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/cac9a3798f1b94319c235b7f8cfb6e8a.png)
![\frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8} \frac{\sqrt[]{2}\left(2+\sqrt[]{2}-\sqrt[]{6} \right)}{8}](/latexrender/pictures/b718adb676d85bd6a07de8227a184f2c.png)
![\frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8} \frac{2\sqrt[]{2} + \sqrt[]{4} - \sqrt[]{12}}{8}](/latexrender/pictures/0e5bdd978030cae907a3e02b0030ab84.png)
![\frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4} \frac{1\sqrt[]{2} + 2 - 2\sqrt[]{3}}{4}](/latexrender/pictures/3454c7f7d32112ae8d1ac43ee1530022.png)
![\frac{1\sqrt[]{2} +\sqrt[]{3}}{4} \frac{1\sqrt[]{2} +\sqrt[]{3}}{4}](/latexrender/pictures/d5a98b1546baaf13361a9b667131bd8a.png)
![\frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}} \frac{4\sqrt[6]{{8}^{3}}- 2\sqrt[6]{{18}^{3}}}{\sqrt[6]{{2}^{2}}}](/latexrender/pictures/2fe825db061b644fcd2f356f18281527.png)
![\left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right) \left(\sqrt[3]{27}-2\sqrt[3]{9}+5 \right) - \left(\sqrt[3]{27}+2\sqrt[3]{81}-2 \right)](/latexrender/pictures/0093ba7dd8b9eff58a02eeb302c78d8d.png)
![\left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right) \left(3 -2\sqrt[3]{9}+5 \right) - \left(3 - 2\sqrt[3]{81} - 2 \right)](/latexrender/pictures/926aded02e900b2d0046c389e539665c.png)





![\frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}} \frac{4\sqrt[6]{8^3}- 2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = \frac{4\sqrt[6]{8^3}}{\sqrt[6]{2^2}} - \frac{2\sqrt[6]{18^3}}{\sqrt[6]{2^2}} = 4\sqrt[6]{\frac{8^3}{2^2}} - 2\sqrt[6]{\frac{18^3}{2^2}}](/latexrender/pictures/936249e25498e25ffbc85ec40ccf9e85.png)
![\left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right) \left(\sqrt[3]{27} -2\sqrt[3]{9} - 5\sqrt[3]{3} \right) - \left(\sqrt[3]{27} + 2\sqrt[3]{81} - 2\sqrt[3]{9} \right)](/latexrender/pictures/f39a8b6cf602d2758e5f7b757e9479a1.png)
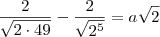

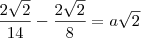


![=\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2} =\frac{\left[\left(\sqrt{3}\right)^2+2\sqrt{3} + 1^2\right] + \left[\left(\sqrt{3}\right)^2-2\sqrt{3} + 1^2\right]}{\left(\sqrt{3}\right)^2 - 1^2}](/latexrender/pictures/b62ef232b3674806c0f276037e45d7fb.png)
![\left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right) \left(3-2\sqrt[3]{9}+5\sqrt[3]{3} \right) - \left(3+6\sqrt[3]{3} - 2\sqrt[3]{9} \right)](/latexrender/pictures/603e6c34ffaaf530b8bc4084fa9166d8.png)
![3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9} 3-2\sqrt[3]{9}+5\sqrt[3]{3} -3 -6\sqrt[3]{3} + 2\sqrt[3]{9}](/latexrender/pictures/1fd2549717861a7aee748b413dbf44ba.png)
![+5\sqrt[3]{3}-6\sqrt[3]{3} +5\sqrt[3]{3}-6\sqrt[3]{3}](/latexrender/pictures/2817cd9c822e3020313b94124bf7bf22.png)
![\frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1} \frac{\left(3+2\sqrt[]{3} +1 \right) + \left(3-2\sqrt[]{3}+1 \right)}{3-1}](/latexrender/pictures/9978dfe8da24d6a95f69665fbe2efc91.png)
![\frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2} \frac{\left(4+2\sqrt[]{3} \right) + \left(4-2\sqrt[]{3}\right)}{2}](/latexrender/pictures/e9f3f7b194d0c196123ade0305daab6a.png)
 =
= 
![-5\sqrt[3]{3} -5\sqrt[3]{3}](/latexrender/pictures/f482f41c1d4790fa1a76fe2473035097.png) e não
e não ![5\sqrt[3]{3} 5\sqrt[3]{3}](/latexrender/pictures/58a6fc46f0845e880cd6aef6fcb091ab.png) como você escreveu.
como você escreveu.![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} - 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/a329addd67fe6089d0876a9c982c0330.png) é equivalente a
é equivalente a ![-11\sqrt[3]{3} -11\sqrt[3]{3}](/latexrender/pictures/10a3a4eb8435cdf802dcd3336b920906.png) .
.![\sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right) \sqrt[3]{3}\left(\sqrt[3]{9} -2\sqrt[3]{3} + 5 \right) - \sqrt[3]{9}\left(\sqrt[3]{3} + 2\sqrt[3]{9} - 2 \right)](/latexrender/pictures/1b7856884e6cd6ce09155ac944ea401e.png) é equivalente a
é equivalente a 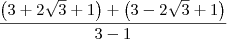
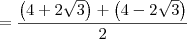



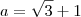 e
e 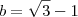 .
.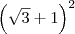 ;
;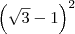 ;
;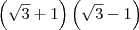 .
.