 por moyses » Ter Fev 07, 2012 12:44
por moyses » Ter Fev 07, 2012 12:44
ola pessoal mais uma vez eu aqui de novo poeguntando pra vocês kkkk

lá vai:
33(FGV-SP) Resolva, no campo real, as equações:
A)

B)
![\sqrt[]{3x+4}-x=-8 \sqrt[]{3x+4}-x=-8](/latexrender/pictures/1e51fa8829ee9861eab20a39a4718692.png)
bom a letra A) eu consigui fazer
![5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1 5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1](/latexrender/pictures/8ae382cf6037d9f7188e3b99aa847fac.png)
mais a letra B) nem consigui ?? como fazer a letra B) me ajudem ai pessoal fazendo favor

-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Fev 07, 2012 13:33
por LuizAquino » Ter Fev 07, 2012 13:33
moyses escreveu:33(FGV-SP) Resolva, no campo real, as equações:
A)

B)

bom a letra A) eu consigui fazer
![5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1 5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1](/latexrender/pictures/8ae382cf6037d9f7188e3b99aa847fac.png)
mais a letra B) nem consigui ?? como fazer a letra B) me ajudem ai pessoal fazendo favor

Por favor, vide a página abaixo e tente terminar o exercício:
Equações Irracionaishttp://www.brasilescola.com/matematica/ ... ionais.htm
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Ter Fev 07, 2012 15:29
por moyses » Ter Fev 07, 2012 15:29
obrigado a todos vou tentar....

assim que possivel eu posto o resultado!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por moyses » Qui Fev 09, 2012 16:57
por moyses » Qui Fev 09, 2012 16:57

|||AGORA ENTENDI, QUANDO A EQUAÇÃO TIVER UM RAIZ COM INCÓGNITA, BASTA ISOLAR O RADICANDO E ELEVAR AMBOS OS TERMOS AO QUADRADO||| huhu.. continuando agora tudo aquilo se tornou uma equação simples do 2° grau que da hora hahah usando a formula de bhaskara temos:
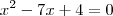
A=1,B=-7, C=4
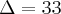
,
![\frac{7 + \sqrt[]{33}}{2} \frac{7 + \sqrt[]{33}}{2}](/latexrender/pictures/c740b24fdd72872289f68ed696967e60.png)
ou
![\frac{7 - \sqrt[]{33}}{2} \frac{7 - \sqrt[]{33}}{2}](/latexrender/pictures/20fd2ce8ea8f6b5f45392bd87e42128e.png)
então
![V=( \frac{7 - \sqrt[]{33}}{2} , \frac{7 + \sqrt[]{33}}{2}) V=( \frac{7 - \sqrt[]{33}}{2} , \frac{7 + \sqrt[]{33}}{2})](/latexrender/pictures/307b1efb2c34f64056b5fadc309222be.png)
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Fev 09, 2012 17:09
por LuizAquino » Qui Fev 09, 2012 17:09
moyses escreveu:
Você errou o desenvolvimento.
O correto seria:

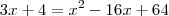

Resolvendo essa equação, encontramos x = 15 e x = 4.
Agora devemos testar esses valores na equação original.
(i) para x = 15.

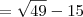
= 7 - 15 = -8
A equação é atendida.
(i) para x = 4.


= 4 - 4 = 0
A equação não é atendida (já que o valor final foi diferente de -8).
Conclusão: o conjunto solução da equação é S={15}.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por moyses » Qui Fev 09, 2012 20:32
por moyses » Qui Fev 09, 2012 20:32
nossa obrigado eu nem percebi kkkkk na anciedade de respoder corretamente kkkk, mias obrigado mesmo assim mesmo aqora eu sei resolver equaçoes de racionalização!
-
moyses
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Seg Ago 29, 2011 09:55
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: SISTEMA DE INFORMAÇÃO
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- EQUAÇÕES NO CONJUNTO DOS REAIS
por jose henrique » Seg Set 06, 2010 22:24
- 1 Respostas
- 1760 Exibições
- Última mensagem por Douglasm

Seg Set 06, 2010 23:15
Álgebra Elementar
-
- conjuntos formados por equações
por Guga1981 » Dom Jan 18, 2015 13:50
- 5 Respostas
- 2439 Exibições
- Última mensagem por DanielFerreira

Qui Jan 22, 2015 18:48
Conjuntos
-
- Conjuntos formados por equações (2)
por Guga1981 » Dom Jan 18, 2015 14:03
- 2 Respostas
- 1891 Exibições
- Última mensagem por Guga1981

Ter Jan 20, 2015 01:55
Conjuntos
-
- zeros reais de funções reais
por bebelo32 » Dom Mar 11, 2018 21:12
- 2 Respostas
- 5508 Exibições
- Última mensagem por adauto martins

Seg Abr 23, 2018 17:52
Funções
-
- Conjuntos, Relações, Equações e Função Quadrática
 por angeloka » Qui Out 21, 2010 21:17
por angeloka » Qui Out 21, 2010 21:17
- 12 Respostas
- 9103 Exibições
- Última mensagem por francisca

Seg Nov 22, 2010 10:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\sqrt[]{3x+4}-x=-8 \sqrt[]{3x+4}-x=-8](/latexrender/pictures/1e51fa8829ee9861eab20a39a4718692.png)
![5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1 5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1](/latexrender/pictures/8ae382cf6037d9f7188e3b99aa847fac.png)



![\sqrt[]{3x+4}-x=-8 \sqrt[]{3x+4}-x=-8](/latexrender/pictures/1e51fa8829ee9861eab20a39a4718692.png)
![5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1 5.{(1+x)}^{5}=20\Rightarrow{(1+x)}^{5}=4\Rightarrow x=\sqrt[5]{4}-1](/latexrender/pictures/8ae382cf6037d9f7188e3b99aa847fac.png)



 assim que possivel eu posto o resultado!
assim que possivel eu posto o resultado!
 |||AGORA ENTENDI, QUANDO A EQUAÇÃO TIVER UM RAIZ COM INCÓGNITA, BASTA ISOLAR O RADICANDO E ELEVAR AMBOS OS TERMOS AO QUADRADO||| huhu.. continuando agora tudo aquilo se tornou uma equação simples do 2° grau que da hora hahah usando a formula de bhaskara temos:
|||AGORA ENTENDI, QUANDO A EQUAÇÃO TIVER UM RAIZ COM INCÓGNITA, BASTA ISOLAR O RADICANDO E ELEVAR AMBOS OS TERMOS AO QUADRADO||| huhu.. continuando agora tudo aquilo se tornou uma equação simples do 2° grau que da hora hahah usando a formula de bhaskara temos: 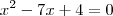 A=1,B=-7, C=4
A=1,B=-7, C=4 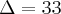 ,
, ![\frac{7 + \sqrt[]{33}}{2} \frac{7 + \sqrt[]{33}}{2}](/latexrender/pictures/c740b24fdd72872289f68ed696967e60.png) ou
ou ![\frac{7 - \sqrt[]{33}}{2} \frac{7 - \sqrt[]{33}}{2}](/latexrender/pictures/20fd2ce8ea8f6b5f45392bd87e42128e.png) então
então ![V=( \frac{7 - \sqrt[]{33}}{2} , \frac{7 + \sqrt[]{33}}{2}) V=( \frac{7 - \sqrt[]{33}}{2} , \frac{7 + \sqrt[]{33}}{2})](/latexrender/pictures/307b1efb2c34f64056b5fadc309222be.png)


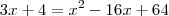


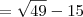






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.