Boa noite!
Gostaria de saber como calcular limites de sucessões definidas por recorrência...
Abraço,
Pedro Oliveira





matpet92 escreveu:O enunciado apresenta uma sucessão definida por recorrência e diz:
Primeiro termo da sucessão (Un) é igual a raiz quadrada(2).
Também que o termo seguinte pode ser obtido pelas raiz quadrada(2Un),ou seja,Un+1=raiz quandrada 2Un.
E a questão é: Calcule o limite da sucessão.
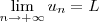 .
.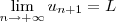 .
.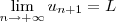

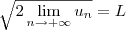



 ), concluímos que L = 2.
), concluímos que L = 2. .
.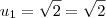
![u_2 = \sqrt{2u_1} = \sqrt{2\sqrt{2}} = \sqrt[4]{2^3} u_2 = \sqrt{2u_1} = \sqrt{2\sqrt{2}} = \sqrt[4]{2^3}](/latexrender/pictures/1c02151d485f92c47b65b8fbfd6fd385.png)
![u_3 = \sqrt{2u_2} = \sqrt{2\sqrt[4]{2^3}} = \sqrt[8]{2^7} u_3 = \sqrt{2u_2} = \sqrt{2\sqrt[4]{2^3}} = \sqrt[8]{2^7}](/latexrender/pictures/7c025b485b086cc540b74262deb3c991.png)
![u_4 = \sqrt{2u_3} = \sqrt{2\sqrt[8]{2^7}} = \sqrt[16]{2^{15}} u_4 = \sqrt{2u_3} = \sqrt{2\sqrt[8]{2^7}} = \sqrt[16]{2^{15}}](/latexrender/pictures/7286ef7e4b1a8e17f5171143e1300fe7.png)
![u_n = \sqrt[2^n]{2^{2^n - 1}} u_n = \sqrt[2^n]{2^{2^n - 1}}](/latexrender/pictures/9f9f77c7110c3037f30976bb5213c4fa.png)
![\lim_{n\to +\infty} u_{n} = \lim_{n\to +\infty} \sqrt[2^n]{2^{2^n - 1}} \lim_{n\to +\infty} u_{n} = \lim_{n\to +\infty} \sqrt[2^n]{2^{2^n - 1}}](/latexrender/pictures/2f11affc6bb1cf33e682bc8c474af01a.png)
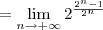
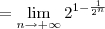



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.
 :
: