Um plano fica dividido em duas regiões quando traçamos uma reta (contida nesse plano). Se traçarmos duas retas nesse plano podemos dividi-lo, em no máximo, 4 regiões, com três retas podemos determinar, no máximo, 7 regiões.
a) (1,0) Complete a tabela:
Retas no plano 1 2 3 4 5 6 7
Quantidade máxima de
regiões obtidas 2 4 7
b) (1,5) Escreva a fórmula de recorrência da sequência que fornece a quantidade máxima de regiões, an, que podem ser obtidas com n retas, explique seu raciocínio.
A fórmula geral, que fornece a quantidade máxima de regiões para n retas é dada por: , onde n é a quantidade de retas e an é a quantidade máxima de regiões.
c) (1,0) Verifique se essa fórmula está de acordo com os valores da tabela do item 'a', deixe seus cálculos registrados como justificativa.
Por favor alguem pode me ajudar a resolver?
Queria uma explicação, pois nao consigo entender esse conteudo.




 .
.
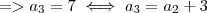 .
.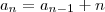 . Já a quantidade máxima de regiões para n retas é data por
. Já a quantidade máxima de regiões para n retas é data por 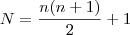 ( para provar essa relação pode-se usar Indução Finita ) .
( para provar essa relação pode-se usar Indução Finita ) .