por Keleber » Sex Fev 03, 2012 16:05
por LuizAquino » Sex Fev 03, 2012 21:37
Keleber escreveu:Eu gostaria de saber como se processa uma derivada de vários produtos: Como esta:
(f(x)g(x)H(x)L(x))´.
![[f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime](/latexrender/pictures/fbf824199dcd1acfb6963dd9b6fc1fd5.png "[f(x)g(x)h(x)l(x)]^\prime = [f(x)g(x)]^\prime[h(x)l(x)] + [f(x)g(x)][h(x)l(x)]^\prime")
![=[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)]](/latexrender/pictures/a9034c05257b995eb3afd829c3aeab2a.png "=[f^\prime(x)g(x) + f(x)g^\prime(x)][h(x)l(x)] + [f(x)g(x)][h^\prime(x)l(x) + h(x)l^\prime(x)]")
Keleber escreveu:Por exemplo: qual a derivada de:
x²x³x. ou também, já que é de praxe usar senos e cosenos: (sen(x)cos(x)tang(x))´ e outras mais que puderem exemplificar.
por ant_dii » Sex Fev 03, 2012 21:42
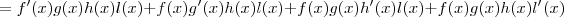
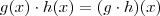.![(f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh'](/latexrender/pictures/6efa23362c756b902c93ed729beba150.png "(f\cdot g \cdot h)'=[f\cdot(gh)]'=f'(gh)+f(gh)'=f'gh+f(g'h+gh')=f'gh+fg'h+fgh'")
por ant_dii » Sex Fev 03, 2012 21:43
por LuizAquino » Sex Fev 03, 2012 21:49
ant_dii escreveu:Mil desculpas Luiz, não vi que já havia respondido...
por Keleber » Sáb Fev 04, 2012 11:29
Voltar para Cálculo: Limites, Derivadas e Integrais
por concurseironf » Sex Set 05, 2014 18:11
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
(dica : igualar a expressão a 
e elevar ao quadrado os dois lados)