Scheu escreveu:1-
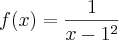
onde devo achar o
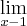
. Tentando resolver cheguei a:
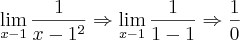
. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
Eu presumo que a função seja
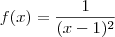
. Além disso, que o limite seja

.
Como você já percebeu, quando

, temos que
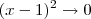
. Sendo assim, temos que:
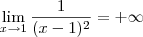
Eu recomendo que você assista a vídeo-aula " 05. Cálculo I - Limites Infinitos" disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquinoScheu escreveu:2- Quanto as indeterminações, peço que me ajude exemplificando todos os métodos possíveis para resolve-las.
a)
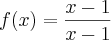
, onde
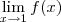
, resolvendo achei:
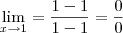
b)
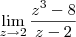
, resolvendo achei:

c)
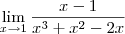
, resolvendo achei:

.
a) Qualquer número (exceto o zero) dividido por ele mesmo é igual a 1. Ou seja,

é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:
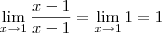
b) Usando o produto notável
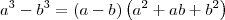
, temos que:
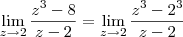
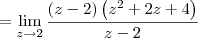
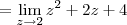
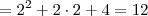
c) Fatorando o polinômio que aparece no denominador, temos que:
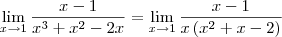
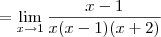
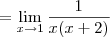
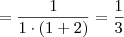 Observação
ObservaçãoPor questão de organização do fórum, nós recomendamos que em cada tópico haja apenas um exercício.
Além disso, vale lembrar que não é objetivo do fórum resolver listas de exercício.
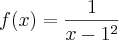 onde devo achar o
onde devo achar o 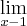 . Tentando resolver cheguei a:
. Tentando resolver cheguei a: 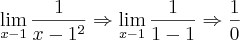 . Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.
. Chegando nesse ponto o professor falou que constitui uma impossibilidade, mas que da para fazer através de jogo de sinais, entretanto ainda não consegui resolver.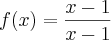 , onde
, onde 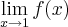 , resolvendo achei:
, resolvendo achei: 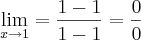

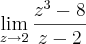 , resolvendo achei:
, resolvendo achei: 
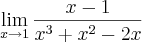 , resolvendo achei:
, resolvendo achei:  .
.

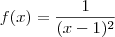 . Além disso, que o limite seja
. Além disso, que o limite seja  .
. , temos que
, temos que 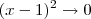 . Sendo assim, temos que:
. Sendo assim, temos que: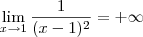
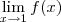 , resolvendo achei:
, resolvendo achei: 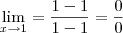
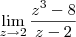 , resolvendo achei:
, resolvendo achei: 
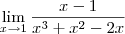 , resolvendo achei:
, resolvendo achei:  é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que:
é sempre igual a 1 (exceto quando a = 0). Desse modo, temos que: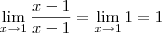
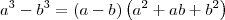 , temos que:
, temos que: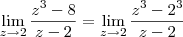
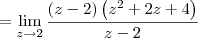
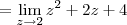
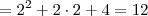
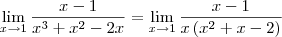
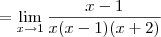
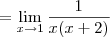
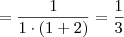


 .
.



