 por Cleyson007 » Sex Set 12, 2008 12:47
por Cleyson007 » Sex Set 12, 2008 12:47
Olá Fabio Sousa, bom dia!!!
Não estou conseguindo resolver o seguinte sistema de equações... Já tentei resolver pelo método da substituição, mas não obtenho a resposta de maneira alguma

!!!
O sistema é o seguinte --->
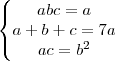
Qual o método de devo utilizar para resolver esse tipo de sistema?

Me dê uma dica por favor!!!

Tenha um bom dia!!!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Sex Set 12, 2008 18:10
por admin » Sex Set 12, 2008 18:10
Olá Cleyson, boa tarde!
Tente por substituição mesmo. Comece substituindo

na primeira equação e continue...
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Set 14, 2008 00:39
por Cleyson007 » Dom Set 14, 2008 00:39
Boa noite Fabio Sousa!!!
Substituindo

na 1ª equação, encontrei a equação

.
Procurei substituir esse valor na 2ª equação ---> Resultando em:

Multiplicando cruzado a equação encontrei:


Gostaria de saber se até aqui está correto.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Ter Set 16, 2008 20:57
por admin » Ter Set 16, 2008 20:57
Olá Cleyson, boa noite!
Acho melhor você não substituir assim

na segunda equação.
Daqui:
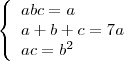
Considere apenas:
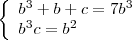
E resolva:
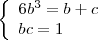
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Seg Jun 01, 2009 12:18
por Cleyson007 » Seg Jun 01, 2009 12:18
fabiosousa escreveu:Olá Cleyson, boa noite!
E resolva:
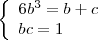
Bom dia Fabio Sousa!
Estou revendo alguns tópicos que ficaram "pendentes".
Quanto a citação acima, entendi a "origem" das equações.
Agora, partindo para a resolução:
Da segunda equação, encontrei o valor de

:

Substitiuindo o valor de

na primeira equação, estou encontrando:

Resolvendo:
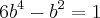
Resolvendo pelo Fator Comum:

Para encontrar o valor de

, estou igualando "as duas partes" a 1
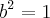


Igualando o parêntese (segunda parte)-->
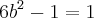
![b=\frac{\sqrt[2]{3}}{3} b=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/3c99da2c8444ea470819decb455fa6bc.png)
Até aqui está correto?
Aguardo sua ajuda.
Um abraço.
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por negrinha » Qua Jun 03, 2009 16:59
por negrinha » Qua Jun 03, 2009 16:59
Cleyson....por favor me ajuda....
Uma industria implantou um programa de prevenção de acidentes de trabalho. Esse programa prevê que o numero y de acidentes varie em funçao do tempo t (em anos) de acordo com a lei y=43.0-3.6 t. Nessas condições, quantos anos essa industria levará para erradicar os acidentes de trabalho?
-
negrinha
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 03, 2009 16:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Cleyson007 » Qua Jun 03, 2009 17:25
por Cleyson007 » Qua Jun 03, 2009 17:25
Boa tarde!
Primeiramente, seja bem-vinda ao Ajuda Matemática!
Por favor, a fim de manter o fórum organizado, abra um novo tópico para cada dúvida que tiver, ok?
Quanto a sua dúvida, a função seria essa-->

?
Abra um novo tópico para questão!
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4491 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3343 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3590 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
-
- Sistema de equações
por D7Sousa » Sáb Abr 24, 2010 12:45
- 3 Respostas
- 2201 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 18:17
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 !!!
!!!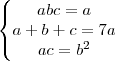
 Me dê uma dica por favor!!!
Me dê uma dica por favor!!! 


 na primeira equação e continue...
na primeira equação e continue...
 .
.

 na segunda equação.
na segunda equação.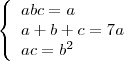
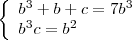
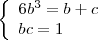


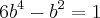

 , estou igualando "as duas partes" a 1
, estou igualando "as duas partes" a 1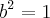


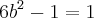
![b=\frac{\sqrt[2]{3}}{3} b=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/3c99da2c8444ea470819decb455fa6bc.png)

 ?
?




