 por Cleyson007 » Sex Set 12, 2008 12:47
por Cleyson007 » Sex Set 12, 2008 12:47
Olá Fabio Sousa, bom dia!!!
Não estou conseguindo resolver o seguinte sistema de equações... Já tentei resolver pelo método da substituição, mas não obtenho a resposta de maneira alguma

!!!
O sistema é o seguinte --->
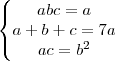
Qual o método de devo utilizar para resolver esse tipo de sistema?

Me dê uma dica por favor!!!

Tenha um bom dia!!!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Sex Set 12, 2008 18:10
por admin » Sex Set 12, 2008 18:10
Olá Cleyson, boa tarde!
Tente por substituição mesmo. Comece substituindo

na primeira equação e continue...
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Dom Set 14, 2008 00:39
por Cleyson007 » Dom Set 14, 2008 00:39
Boa noite Fabio Sousa!!!
Substituindo

na 1ª equação, encontrei a equação

.
Procurei substituir esse valor na 2ª equação ---> Resultando em:

Multiplicando cruzado a equação encontrei:


Gostaria de saber se até aqui está correto.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Ter Set 16, 2008 20:57
por admin » Ter Set 16, 2008 20:57
Olá Cleyson, boa noite!
Acho melhor você não substituir assim

na segunda equação.
Daqui:
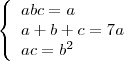
Considere apenas:
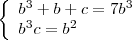
E resolva:
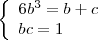
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Seg Jun 01, 2009 12:18
por Cleyson007 » Seg Jun 01, 2009 12:18
fabiosousa escreveu:Olá Cleyson, boa noite!
E resolva:
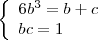
Bom dia Fabio Sousa!
Estou revendo alguns tópicos que ficaram "pendentes".
Quanto a citação acima, entendi a "origem" das equações.
Agora, partindo para a resolução:
Da segunda equação, encontrei o valor de

:

Substitiuindo o valor de

na primeira equação, estou encontrando:

Resolvendo:
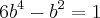
Resolvendo pelo Fator Comum:

Para encontrar o valor de

, estou igualando "as duas partes" a 1
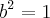


Igualando o parêntese (segunda parte)-->
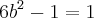
![b=\frac{\sqrt[2]{3}}{3} b=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/3c99da2c8444ea470819decb455fa6bc.png)
Até aqui está correto?
Aguardo sua ajuda.
Um abraço.
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por negrinha » Qua Jun 03, 2009 16:59
por negrinha » Qua Jun 03, 2009 16:59
Cleyson....por favor me ajuda....
Uma industria implantou um programa de prevenção de acidentes de trabalho. Esse programa prevê que o numero y de acidentes varie em funçao do tempo t (em anos) de acordo com a lei y=43.0-3.6 t. Nessas condições, quantos anos essa industria levará para erradicar os acidentes de trabalho?
-
negrinha
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Jun 03, 2009 16:30
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Cleyson007 » Qua Jun 03, 2009 17:25
por Cleyson007 » Qua Jun 03, 2009 17:25
Boa tarde!
Primeiramente, seja bem-vinda ao Ajuda Matemática!
Por favor, a fim de manter o fórum organizado, abra um novo tópico para cada dúvida que tiver, ok?
Quanto a sua dúvida, a função seria essa-->

?
Abra um novo tópico para questão!
Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4494 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3344 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3591 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
-
- Sistema de equações
por D7Sousa » Sáb Abr 24, 2010 12:45
- 3 Respostas
- 2204 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 18:17
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 !!!
!!!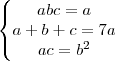
 Me dê uma dica por favor!!!
Me dê uma dica por favor!!! 


 na primeira equação e continue...
na primeira equação e continue...
 .
.

 na segunda equação.
na segunda equação.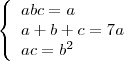
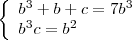
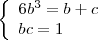


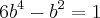

 , estou igualando "as duas partes" a 1
, estou igualando "as duas partes" a 1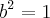


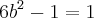
![b=\frac{\sqrt[2]{3}}{3} b=\frac{\sqrt[2]{3}}{3}](/latexrender/pictures/3c99da2c8444ea470819decb455fa6bc.png)

 ?
?

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.