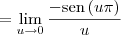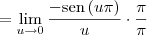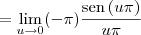por lipelfnc » Qua Jan 25, 2012 20:16
por lipelfnc » Qua Jan 25, 2012 20:16
Primeiros dois exercícios, "de calcular mesmo", do guidorizzi que empaquei. De resto, só os de demonstração que estão me pegando mesmo.
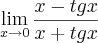
Tentei substituir tgx = senx/cosx, mas travei quando corta os cosx
No gabarito diz que o resultado é 0.
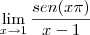
Nesse tentei de vários jeitos, inclusive com a propriedade do limite fundamental.
E obrigado pelas dicas quanto aos exercícios de demonstração.
-
lipelfnc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jan 24, 2012 14:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng/Programação
- Andamento: formado
 por lipelfnc » Qua Jan 25, 2012 22:23
por lipelfnc » Qua Jan 25, 2012 22:23
Nossa, obrigado.
Nunca que eu iria pensar em dividir por x na primeira, e fazer aquela substituição na segunda.
Assim, qual é o segredo para ter essas sacadas? Só a experiência mesmo?
Alguns colegas recomendaram que eu desse uma estudada pelo Apostol. Sei que ele é bem puxado, mas vcs recomendariam para alguem que estará cursando Engenharia?
-
lipelfnc
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jan 24, 2012 14:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng/Programação
- Andamento: formado
 por LuizAquino » Qua Jan 25, 2012 22:46
por LuizAquino » Qua Jan 25, 2012 22:46
lipelfnc escreveu:Assim, qual é o segredo para ter essas sacadas? Só a experiência mesmo?
Sim, com a experiência essas simplificações se tornam naturais.
lipelfnc escreveu:Alguns colegas recomendaram que eu desse uma estudada pelo Apostol. Sei que ele é bem puxado, mas vcs recomendariam para alguem que estará cursando Engenharia?
Para um aluno do curso de Engenharia, eu recomendo a referência abaixo.
- Stewart, James. Cálculo. Vol. I. 6ª Edição. São Paulo: Thomson Pioneira, 2009.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dificuldade em exercícios de demonstração
por lipelfnc » Ter Jan 24, 2012 14:34
- 3 Respostas
- 2853 Exibições
- Última mensagem por fraol

Ter Jan 24, 2012 19:15
Cálculo: Limites, Derivadas e Integrais
-
- [Elipse, hipérbole, parábola] Dificuldade em exercícios!
por geo_nascimento » Dom Out 23, 2011 15:47
- 1 Respostas
- 4930 Exibições
- Última mensagem por LuizAquino

Seg Out 24, 2011 16:33
Geometria Analítica
-
- Demonstração de exercícios
por andrecezar » Qui Mai 18, 2017 00:06
- 0 Respostas
- 2190 Exibições
- Última mensagem por andrecezar

Qui Mai 18, 2017 00:06
Conjuntos
-
- [Álgebra I, exercicios] Exercicios que estão sem resolução.
por vitorullmann » Ter Mar 05, 2013 21:26
- 0 Respostas
- 3292 Exibições
- Última mensagem por vitorullmann

Ter Mar 05, 2013 21:26
Álgebra Elementar
-
- Dificuldade
por Alison Bissoli » Qui Dez 03, 2009 13:40
- 6 Respostas
- 3802 Exibições
- Última mensagem por Elcioschin

Dom Dez 06, 2009 13:54
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
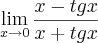
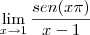

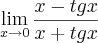
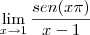

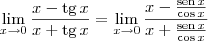
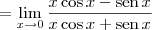
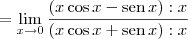

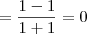
 temos que
temos que  .
.![\lim_{x \to 1}\frac{\textrm{sen}\,(x\pi)}{x - 1} = \lim_{u \to 0}\frac{\textrm{sen}\,[(u+1)\pi]}{u} \lim_{x \to 1}\frac{\textrm{sen}\,(x\pi)}{x - 1} = \lim_{u \to 0}\frac{\textrm{sen}\,[(u+1)\pi]}{u}](/latexrender/pictures/14590523b31f01155ee2d6abd4741114.png)