 por lourivallobo » Qua Jan 25, 2012 09:13
por lourivallobo » Qua Jan 25, 2012 09:13
Pessoal alguém pode me ajudar com relação a questão 18 da prova em anexo?
- Anexos
-
[O anexo não pode ser exibido, pois a extensão pdf foi desativada pelo administrador.]
-
lourivallobo
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Jan 24, 2012 20:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Telecomunicações
- Andamento: formado
 por LuizAquino » Qua Jan 25, 2012 11:05
por LuizAquino » Qua Jan 25, 2012 11:05
lourivallobo escreveu:Pessoal alguém pode me ajudar com relação a questão 18 da prova em anexo?
Por favor, escreva todo o texto do exercício na sua mensagem.
Quando você envia apenas um arquivo com a questão, ela não poderá ser encontrada pelo sistema de busca do fórum, o que prejudica o bom funcionamento do mesmo.
ObservaçãoPara inserir uma matriz na sua mensagem use o seguinte código LaTeX:
- Código: Selecionar todos
[tex]
\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{bmatrix}
[/tex]
O resultado desse código seria:
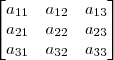
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Qua Jan 25, 2012 14:50
por Arkanus Darondra » Qua Jan 25, 2012 14:50
lourivallobo escreveu:A matriz

é tal que
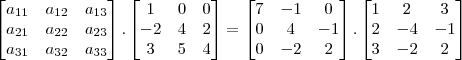
O determinante da matriz

é igual a:
(A) -6
(B) 0
(C) 6
(D) 10
(E) 42
Consegui chegar que o
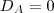
, ficou bem trabalhoso, mas não tenho certeza da resposta:
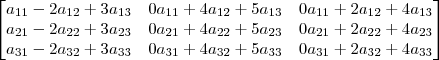


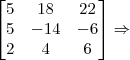 Monte um sistema e encontrará
Monte um sistema e encontrará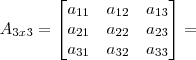

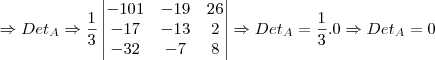
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por LuizAquino » Qua Jan 25, 2012 17:12
por LuizAquino » Qua Jan 25, 2012 17:12
Arkanus Darondra escreveu:Consegui chegar que o
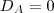
, ficou bem trabalhoso, mas não tenho certeza da resposta:
Lembre-se da propriedade:
det(AB) = (det A)(det B)
Desse modo, temos que:




-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Arkanus Darondra » Qua Jan 25, 2012 17:30
por Arkanus Darondra » Qua Jan 25, 2012 17:30
LuizAquino escreveu:Lembre-se da propriedade:
det(AB) = (det A)(det B)
Verdade. Assim fica bem mais simples o cálculo.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Matrizes e Determinantes
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Concurso Petrobras
 por lourivallobo » Ter Jan 24, 2012 20:47
por lourivallobo » Ter Jan 24, 2012 20:47
- 1 Respostas
- 3955 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:12
Logaritmos
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:49
- 1 Respostas
- 1446 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 21:51
Estatística
-
- Concurso Petrobras
por lourivallobo » Ter Jan 24, 2012 20:52
- 1 Respostas
- 3011 Exibições
- Última mensagem por LuizAquino

Ter Jan 24, 2012 22:08
Estatística
-
- PA concurso petrobras
por thiagodr » Sex Mar 23, 2012 01:07
- 3 Respostas
- 2002 Exibições
- Última mensagem por thiagodr

Sáb Abr 07, 2012 16:34
Progressões
-
- DERIVADA - CONCURSO PETROBRAS
por pinkfluor » Qua Mar 02, 2011 11:10
- 2 Respostas
- 2319 Exibições
- Última mensagem por LuizAquino

Qua Mar 02, 2011 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



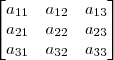

é tal que
é igual a:
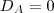 , ficou bem trabalhoso, mas não tenho certeza da resposta:
, ficou bem trabalhoso, mas não tenho certeza da resposta: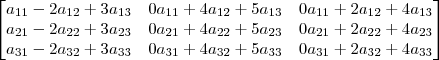


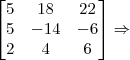 Monte um sistema e encontrará
Monte um sistema e encontrará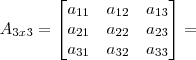

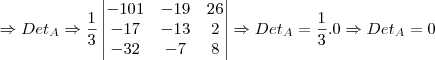

, ficou bem trabalhoso, mas não tenho certeza da resposta:












