 por Arkanus Darondra » Seg Jan 23, 2012 19:37
por Arkanus Darondra » Seg Jan 23, 2012 19:37
Boa Tarde!
Andrewo escreveu:Exercícios que nao consigo fazer:
1º -

-

+ a + b
Temos aí uma diferença de quadrados
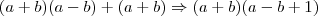
Andrewo escreveu:2º - 2

+

- 6x -
A julgar pelo gabarito. Creio que seja
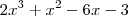
. Sendo assim:
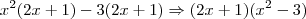
Andrewo escreveu:3º - 14yz - 28zx + 6y - 12x
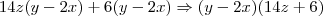
Colocando o 2 em evidência:
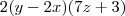
Qualquer dúvida...

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Andrewo » Ter Jan 24, 2012 11:44
por Andrewo » Ter Jan 24, 2012 11:44
Vlw mano, ajudou mto
Uma dúvida, nessa conta
Arkanus Darondra escreveu:Boa Tarde!
Temos aí uma diferença de quadrados
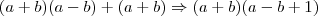
Se eu resolver
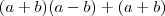
eu vou ficar com

-

+ (a + b) ; já não pararia a fatoração por aí? daonde vem aquele +1 que vc colocou?
Aproveitando o tópico:
Nesse exercício:
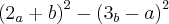
Considerando que é diferença de quadrados e que
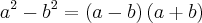
Eu tentei fazer oseguinte :
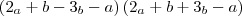

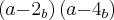
e a resposta pelo gabarito é


Não entendi pq a resposta ficou essa :S
Outra fatoração:
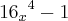 o que eu tentei »
o que eu tentei » 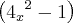
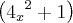
Mas pelo gabarito to errado, a resposta é

De diferença de cubos:
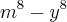
O que eu fiz :
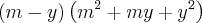
O que o gabarito diz :

E nessa outra fatoração:
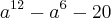
eu fiquei mesmo confuso, quando eu vi a resposta :
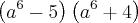
Se for multiplicar dá certo, mas como é diferença de quadrados, 20 nao tem raiz entao colocaram 2 nº diferentes pra multiplicação dar resultado 20, isso tá certo?

-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Ter Jan 24, 2012 12:14
por Arkanus Darondra » Ter Jan 24, 2012 12:14
Andrewo escreveu:Vlw mano, ajudou mto
Uma dúvida, nessa conta
Arkanus Darondra escreveu:Boa Tarde!
Temos aí uma diferença de quadrados
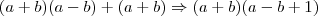
Se eu resolver
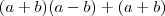
eu vou ficar com

-

+ (a + b) ; já não pararia a fatoração por aí? daonde vem aquele +1 que vc colocou?
Veja que não podemos para por aí, pois ainda há um termo comum: o
(a + b).
O que eu fiz foi apenas colocá-lo em evidencia.
Para ilustrar melhor vou representar de outro modo:
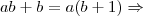
isso explica a origem do
1 
Quanto as outras dúvida, por favor crie outro tópico para elas.
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [fatoração] fatoração de polinômio do quarto grau.
por +Danilo2 » Qui Set 29, 2016 10:43
- 5 Respostas
- 8930 Exibições
- Última mensagem por +Danilo2

Sáb Out 08, 2016 18:17
Polinômios
-
- fatoração de Polinômio fatoração de agrupamento
por Estudante13 » Sex Nov 09, 2012 22:52
- 1 Respostas
- 3264 Exibições
- Última mensagem por Cleyson007

Sex Nov 09, 2012 23:06
Álgebra Elementar
-
- [fatoração] Exercício de Fatoração
por Cleyson007 » Qua Abr 30, 2008 00:39
- 3 Respostas
- 8831 Exibições
- Última mensagem por admin

Qua Abr 30, 2008 02:15
Álgebra Elementar
-
- Fatoração
por Rogerioeetc » Sex Jul 24, 2009 02:00
- 2 Respostas
- 2550 Exibições
- Última mensagem por Rogerioeetc

Dom Jul 26, 2009 14:26
Álgebra Elementar
-
- Fatoração
por Jaqueline Pimenta » Qui Out 01, 2009 11:50
- 5 Respostas
- 4095 Exibições
- Última mensagem por Jaqueline Pimenta

Seg Out 05, 2009 12:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 -
-  + a + b =
+ a + b =  +
+  - 6x -
- 6x -  - 3)
- 3)


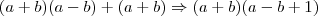
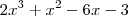 . Sendo assim:
. Sendo assim: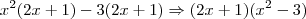
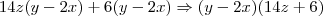
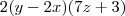

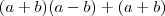 eu vou ficar com
eu vou ficar com 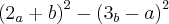
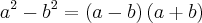
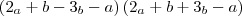

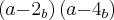


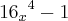
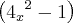
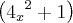

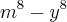
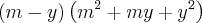

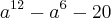
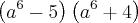
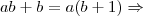 isso explica a origem do
isso explica a origem do