Ops... Desculpem, respondi com pressa e depois fiquei preocupado com a resposta correta... kkkk... Foi malss, mas a resposta certa é a que o Arkanus falou...
Uma desatenção minha, pois estava a sair do trabalho, resolvi responder rapidinho e acabei deixando de concluir... Mas valeu novamente Arkanus, você esta corretíssimo...
Quanto
moyses escreveu:obrigado mais, você poderia me explicar melhor? se não for encomodo

Veja o argumento:
Tomemos um elemento qualquer
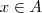
, como

temos que
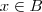
. Da mesma forma, considerando que
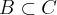
,
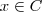
, logo
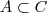
.
Agora tomemos um elemento
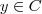
, mas
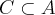
, logo
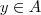
...
Portanto todo elemento de A é elemento de C... Seguindo o mesmo raciocínio você verá que existe essa mesma relação entre A e B, B e C...
Por definição, dois conjuntos são iguais se, e somente se, todo elemento de um é elemento de outro... Formalmente: Dados os conjuntos A e B, quaisquer,
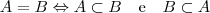
.
Quanto a última observação de Arkanus, na verdade quando se tem que
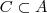
, automaticamente,
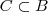
, pois

. Isso indica que, como disse corretamente (e agradeço novamente),
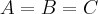
.
Só os loucos sabem...
 ,
, 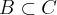 ,
, 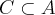 é:
é: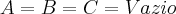
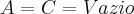
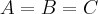
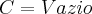

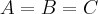 simplesmente por bom senso rsrs
simplesmente por bom senso rsrs  , mais por favor respondam e digam o por que pois eu quero compreender isso , muito obrigado desde já
, mais por favor respondam e digam o por que pois eu quero compreender isso , muito obrigado desde já 


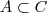 . Como temos
. Como temos 

 , então:
, então:
 . Logo,
. Logo, 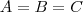

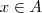 , como
, como 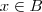 . Da mesma forma, considerando que
. Da mesma forma, considerando que 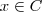 , logo
, logo 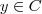 , mas
, mas 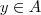 ...
...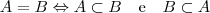 .
.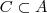 , automaticamente,
, automaticamente, 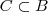 , pois
, pois  . Isso indica que, como disse corretamente (e agradeço novamente),
. Isso indica que, como disse corretamente (e agradeço novamente), 
 , avisa que eu resolvo.
, avisa que eu resolvo.

