Amandinha Bertolin escreveu:Eu tenho um trabalho com 98 questões eu fiz todas mas essas eu nao consegui eu nunca me dei bem com sistemas sera que voce poderia me ajudar?
Vou te dar uma ajuda.
1) Desenvolva o
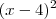
, desse resultado, aplique a distributiva multiplicando tudo por 3
2) Você pode isolar o x ou o y em qualquer uma das duas equações (de preferência na primeira) e substituir na segunda. Após isso, você encontrará o valor de x ou de y. Substitua esse valor em qualquer das duas equações (de preferência na primeira). Outro modo seria multiplicar a primeira equação por -2 ou 5 e somar o resultado com a segunda.
3) Mesmo procedimento (isolar, substituir...)
4) Você pode somá-las que "de cara" cancelará o y. Assim você encontrará o valor de x. Com isso, basta substituir em qualquer das duas equações que você obterá o par ordenado. Agora some-os
5) Somá-las ou isolar. Agora realize xy-2.
6) Isolar e substituir. Ou então multiplicar a primeira equação por -2 e somá-las.
Tente fazer isso, se surgir algum problema, volte aqui.

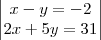 é:
é: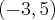
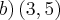
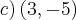
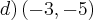
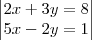 é:
é: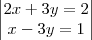 . Então x+y é igual a:
. Então x+y é igual a:

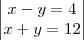 a expressão xy-2 é igual a:
a expressão xy-2 é igual a: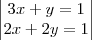 o par ordenado é:
o par ordenado é: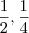
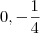
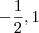
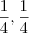



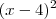 , desse resultado, aplique a distributiva multiplicando tudo por 3
, desse resultado, aplique a distributiva multiplicando tudo por 3
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.