Aqui esta o problema:
A mae da Joana cozinhou no forno um frango do campo para o jantar. Sabe-se que a temperatura do granco, T, em graus Celsius, t minutos após ter sido retirado do forno é dada por:

Quanto tempo decorre entre o instante em que o frango é retirado do forno e instante que a sua temperatiura é de 50ºC?
A solução é 22 minutos e 56 segundos, ainda não percebi como se chega para esse resultado :S





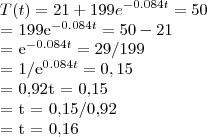

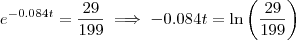
 .Ou seja
.Ou seja  .
.

 .
.
 :
: