
mostre, que
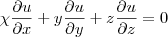
penso que tenho que achar as derivadas parciais,ou seja será que devo de achar o meu A como
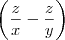 e o B, como
e o B, como  e apartir dai obter
e apartir dai obter  mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção

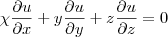
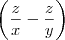 e o B, como
e o B, como  e apartir dai obter
e apartir dai obter  mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
Jorge Dias escreveu:
mostre, que
penso que tenho que achar as derivadas parciais,ou seja será que devo de achar o meu A como
e o B, como
e apartir dai obter
mas não sei como fazer essa derivada e nem o que fazer com a icógnita que está antes da fracção
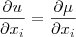
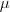 está em função de
está em função de  por
por 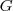 ... E se
... E se  , então você terá que calcular cada derivada em função de uma incógnita de cada vez e depois multiplicar como esta pedindo acima e então procurar uma relação que de zero pra você mostrar o resultado desejado...
, então você terá que calcular cada derivada em função de uma incógnita de cada vez e depois multiplicar como esta pedindo acima e então procurar uma relação que de zero pra você mostrar o resultado desejado... de
de  , é da onde?
, é da onde?
 e então pela regra da cadeia temos
e então pela regra da cadeia temos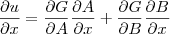

Jorge Dias escreveu:No livro tenho um exemplo que refere assim, sejam A e B as váriáveis mudas associadas á função G, ou seja U= G(A;B)= Ge então pela regra da cadeia temos
e assim sucessivamente para as outras icógnitas y e z é isso o que se pretende? mas não consigo iniciar estas derivadas.
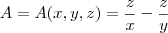

 e faça
e faça  ,
, 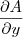 e
e 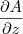 .
.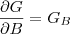 e faça
e faça 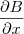 ,
,  e
e 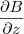 .
.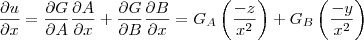
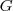 .
.
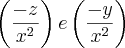 ,não consigo chegar a esse valor
,não consigo chegar a esse valor
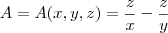 pode ser feita como segue, o mesmo valerá para as outras variáveis e para
pode ser feita como segue, o mesmo valerá para as outras variáveis e para  :
:



ant_dii escreveu:Sim... me desculpe.
A derivada depode ser feita como segue, o mesmo valerá para as outras variáveis e para
:
Quando você deriva em relação a variável precedente as outras se tornam constantes, mas vale as mesmas regras para derivadas com uma variável...
Não sei se esclareceu, mas fique a vontade qualquer dúvida...
 em relação a
em relação a  será usado o mesmo procedimento que foi em relação a
será usado o mesmo procedimento que foi em relação a  (como esta na citação acima), ou seja,
(como esta na citação acima), ou seja,
 em relação a
em relação a  , é feito o seguinte
, é feito o seguinte

 , como já te disse, as outras variáveis se tornam constantes, então
, como já te disse, as outras variáveis se tornam constantes, então  e
e  também são constantes.
também são constantes. , você encontrará os seguintes resultados:
, você encontrará os seguintes resultados: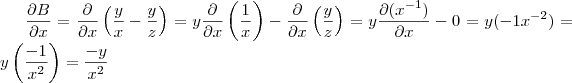
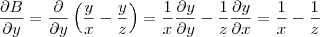
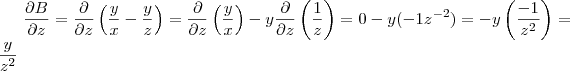
 em relação a cada variável usando os resultados já encontrados:
em relação a cada variável usando os resultados já encontrados: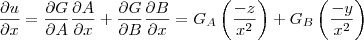

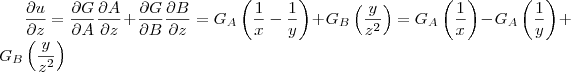



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.