 por joaofonseca » Sáb Jan 07, 2012 11:22
por joaofonseca » Sáb Jan 07, 2012 11:22
Sejam
A,
B e
C três caixas iguais.Em cada uma foram colocadas 10 bolas, umas verdes outras amarelas.
A distribuição é a seguinte:
Caixa
A:
Bolas amarelas: 5
Bolas verdes: 5
Caixa
B:
Bolas amarelas: 2
Bolas verdes: 8
Caixa
C:
Bolas amarelas: 6
Bolas verdes: 4
Escolhendo aleatoriamente uma caixa, qual é a probabilidade de tirar uma bola verde?
Se fosse uma probabilidade condicional, do tipo, qual a probabilidade de tirar bola verde sabendo que se tirou da caixa
A, seria facil.Pois os casos favoraveis limitavam-se às bolas verdes que estão na caixa
A.
Se eu fizer 3 probabilidades condicionadas, cada uma relativa a tirar uma bola de cada uma das caixas, então basta somar as 3 probabilidades condicionadas.Mas isto é a mesma coisa se as 30 bolas estivessem numa unica caixa.Logo:

Será assim?
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Arkanus Darondra » Sáb Jan 07, 2012 12:35
por Arkanus Darondra » Sáb Jan 07, 2012 12:35
Olá joaofonseca,
Embora você tenha chegado à resposta correta, o método que você utilizou não é o "mais correto"
Você chegou à resposta correta porque o número de bolas em cada caixa é o mesmo
Para este tipo de exercício você deve calcular a probabilidade do que se quer, separadamente, e somá-las
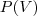
Depois disso, calcular a probabilidade de se escolher uma caixa ao acaso
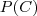
Após isso, basta fazer
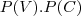
, ou seja,
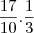
-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Sáb Jan 07, 2012 17:59
por fraol » Sáb Jan 07, 2012 17:59
Concordo com o raciocínio do joaofonseca. Explicitamente teríamos:
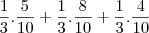
, que é basicamente o que foi dito em
Se eu fizer 3 probabilidades condicionadas, cada uma relativa a tirar uma bola de cada uma das caixas, então basta somar as 3 probabilidades condicionadas.
Arkanus, você colocou probabilidade de
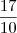
, mas probabilidade, por definição é um número entre 0 e 1.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Arkanus Darondra » Sáb Jan 07, 2012 18:54
por Arkanus Darondra » Sáb Jan 07, 2012 18:54
fraol escreveu:Concordo com o raciocínio do joaofonseca. Explicitamente teríamos:
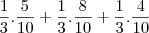
, que é basicamente o que foi dito em
Se eu fizer 3 probabilidades condicionadas, cada uma relativa a tirar uma bola de cada uma das caixas, então basta somar as 3 probabilidades condicionadas.
Concordo, porém ele também afirma:
"(...)isto é a mesma coisa se as 30 bolas estivessem numa unica caixa".
fraol escreveu:Arkanus, você colocou probabilidade de
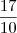
, mas probabilidade, por definição é um número entre 0 e 1.
Concordo, o meu erro foi chamar a soma das probabilidades de P(V), foi um descuido.
Supondo somar 0,8 e 0,7, por exemplo, que são números entre 0 e 1, teremos um número maior que um.
Obrigado pela observação.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10349 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21656 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5349 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4523 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4536 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



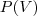
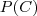
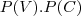 , ou seja,
, ou seja, 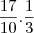
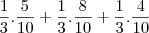 , que é basicamente o que foi dito em
, que é basicamente o que foi dito em 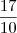 , mas probabilidade, por definição é um número entre 0 e 1.
, mas probabilidade, por definição é um número entre 0 e 1.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
