 por Cleyson007 » Qua Mai 27, 2009 14:01
por Cleyson007 » Qua Mai 27, 2009 14:01
Olá, boa tarde!
Estou encontrando dificuldade para resolver o sistema de equações a seguir. Já tentei resolvê-lo pelo "Método da Substitituição" e pela "Regra de Cramer", mas não obtive êxito. Se alguém puder me dar uma

, agradeço.
--> A partir de

Calcule o valor de
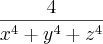
.
Aproveitando a oportunidade, como faço para colocar a "chave" pelo lado esquerdo do sistema?
Agradeço sua ajuda

Até mais
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Molina » Qua Mai 27, 2009 16:46
por Molina » Qua Mai 27, 2009 16:46
Não deu por Cramer?
Estranho.. Vou insistir novamente por esse método e qualquer novidade te informo.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Mai 28, 2009 14:53
por Molina » Qui Mai 28, 2009 14:53
Realmente por Cramer não dá porque o
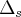
é igual a zero.
To meio sem tempo, infelizmente.
Mas já pensou se ele pode ser
impossível?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Mai 28, 2009 17:51
por Cleyson007 » Qui Mai 28, 2009 17:51
Boa tarde Molina, tudo bem amigo?
Como já disse, estou tentando resolver o sistema usando a "Regra de Cramer". Está ficando assim:
O determinante da matriz incompleta está ficando assim:
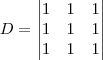
Portanto,

O Determinante de

está ficando assim:

Portanto,

Do mesmo modo fiz os determinantes das matrizes

e

. Encontrando para todos o valor nulo

Com certeza estou errado.... pois seria impossível calcular o valor de
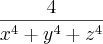
---> O gabarito está apontando como resposta:


Agradeço sua ajuda.
Um abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4491 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5533 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3591 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1554 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
-
- Sistema de equações
por D7Sousa » Sáb Abr 24, 2010 12:45
- 3 Respostas
- 2202 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 18:17
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , agradeço.
, agradeço.
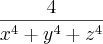 .
.





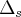 é igual a zero.
é igual a zero.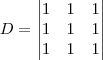

 está ficando assim:
está ficando assim: 

 e
e  . Encontrando para todos o valor nulo
. Encontrando para todos o valor nulo 
